解:(1)由题意可知:抛物线的对称轴为x=1.
当x=1时,y=3x-7=-4,
因此抛物线的顶点M的坐标为(1,-4).
过A(-1,0),B(3,0)
设抛物线的解析式为y=a(x-1)
2-4,
则有:a(3-1)
2-4=0,a=1.
则抛物线的解析式为:y=x
2-2x-3.
(2)根据(1)的抛物线可知:A(-1,0)、B(3,0)、C(0,-3);
易知直线BM的解析式为y=2x-6;
∵当x=t时,y=2t-6;
∴PQ=6-2t;
∴S
四边形PQAC=S
梯形QPCO+S
△AOC=

×(3+6-2t)×t+

×3,即S
四边形PQAC=-t
2+

t+

(1<t<3).
(3)假设存在这样的点N,使△NMC为等腰三角形.
∵点N在BM上,设N点坐标为(m,2m-6),则CM
2=1
2+1
2=2,CN
2=m
2+[-3-(2m-6)]
2,或CN
2=m
2+[(2m-6)+3]
2.
MN
2=(m-1)
2+[4-(6-2m)]
2.△NMC为等腰三角形,有以下三种可能:
①若CN=CM,则m
2+[(6-2m)-3]
2=2,
解得m
1=

,m
2=1(舍去).
则N(
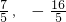
).
②若MC=MN,则(m-1)
2+[4-(6-2m)]
2=1
2+1
2.
解得m=1±

.
∵1<m<3,
∴m=1-

舍去.
∴N(1+
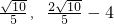
).
③若NC=NM,则m
2+[3-(6-2m)]
2=(m-1)
2+[4-(6-2m)]
2.
解得m=2.
则N(2,-2).
故存在这样的点N,使△NMC为等腰三角形.且点N的坐标分别为:
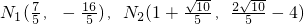
,N
3(2,-2).
分析:(1)根据抛物线与x的两个交点的横坐标可以推知该抛物线的对称轴方程x=1,结合该抛物线的顶点在直线y=3x-7上可以求得该抛物线的顶点坐标是(1,-4).故可设该抛物线的解析式为顶点式方程y=a(x-1)
2-4;最后利用待定系数法可求该抛物线的解析式;
(2)由(1)中的抛物线解析式可以求得点A、B、C的坐标;根据B、M两点的坐标可以求得直线BM的解析式y=2x-6;由该解析式可以求得PQ=6-2t;最后图形可知
S
四边形PQAC=S
梯形QPCO+S
△AOC;
(3)利用反证法解答:假设存在这样的点N,使△NMC为等腰三角形.利用两点间的距离公式分别求得CM、CN、MN的值;然后分类讨论:①MN为底;②CN为底;③CM为底时所求得的点N的坐标.
点评:本题考查了二次函数综合题.注意:△NMC为等腰三角形时,需要分三种情况进行讨论,以防漏解.

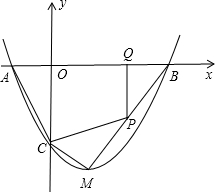 如图,抛物线y=ax2+bx+c与x轴交于A、B两点的横坐标分别是-1,3 (点A在点B左侧),与y轴交于点C,抛物线的顶点M在直线y=3x-7上.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点的横坐标分别是-1,3 (点A在点B左侧),与y轴交于点C,抛物线的顶点M在直线y=3x-7上. ×(3+6-2t)×t+
×(3+6-2t)×t+ ×3,即S四边形PQAC=-t2+
×3,即S四边形PQAC=-t2+ t+
t+ (1<t<3).
(1<t<3). ,m2=1(舍去).
,m2=1(舍去).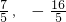 ).
). .
. 舍去.
舍去.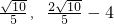 ).
).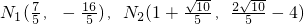 ,N3(2,-2).
,N3(2,-2).

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).