
ΓΨΧβΡΩΓΩΫϋΡξά¥Θ§Έ“ΙζΚήΕύΒΊ«χ≥÷–χ≥ωœ÷Έμω≤ΧλΤχΘ°Ρ≥…γ«χΈΣΝΥΒς≤ι±Ψ…γ«χΨ”ΟώΕ‘Έμω≤ΧλΤχ÷ς“Σ≥…“ρΒΡ»œ Ε«ιΩωΘ§ΥφΜζΕ‘ΗΟ…γ«χ≤ΩΖ÷Ψ”ΟώΫχ––ΝΥΈ ΨμΒς≤ιΘ§“Σ«σΨ”Οώ¥”ΈεΗω÷ς“Σ≥…“ρ÷–÷Μ―Γ‘ώΤδ÷–ΒΡ“ΜœνΘ§±ΜΒς≤ιΨ”ΟώΕΦΑ¥“Σ«σΧν–¥ΝΥΈ ΨμΘ°…γ«χΕ‘Βς≤ιΫαΙϊΫχ––ΝΥ’ϊάμΘ§Μφ÷ΤΝΥ»γœ¬≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ±μΘ°±ΜΒς≤ιΨ”Οώ―Γ‘ώΗς―Γœν»Υ ΐΆ≥ΦΤ±μ
Έμω≤ΧλΤχΒΡ÷ς“Σ≥…“ρ | ΤΒ ΐΘ®»Υ ΐΘ© |
A¥σΤχΤχ―ΙΒΆΘ§Ω’Τχ≤ΜΝςΕ· | m |
BΒΊΟφΜ“≥Ψ¥σΘ§Ω’Τχ ΣΕ»ΒΆ | 40 |
CΤϊ≥ΒΈ≤Τχ≈≈Ζ≈ | n |
DΙΛ≥ß‘λ≥…ΒΡΈέ»Ψ | 120 |
EΤδΥϊ | 60 |
«κΗυΨίΆΦ±μ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ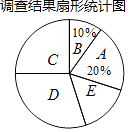
Θ®1Θ©ΧνΩ’ΘΚm= Θ§ n= Θ§ …»–ΈΆ≥ΦΤΆΦ÷–C―ΓœνΥυ’ΦΒΡΑΌΖ÷±»ΈΣ Θ°
Θ®2Θ©»τΗΟ…γ«χΨ”Οώ‘Φ”–6 000»ΥΘ§«κΙάΦΤΤδ÷–Μα―Γ‘ώD―ΓœνΒΡΨ”Οώ»Υ ΐΘ°
Θ®3Θ©Ε‘”ΎΓΑΈμω≤Γ±’βΗωΜΖΨ≥Έ ΧβΘ§«κΡψ”ΟΦρΕΧΒΡ”ο―‘ΖΔ≥ω≥Ϊ“ιΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©80,100,25%
Θ®2Θ©ΫβΘΚ6000ΓΝ ![]() =1800Θ®»ΥΘ©Θ§
=1800Θ®»ΥΘ©Θ§
¥πΘΚΜα―Γ‘ώD―ΓœνΒΡΨ”Οώ»Υ ΐ‘ΦΈΣ1800»Υ
Θ®3Θ©ΫβΘΚΗυΨίΥυ≥ι»Γ―υ±Ψ÷–≥÷CΓΔDΝΫ÷÷ΙέΒψΒΡ»Υ ΐ’ΦΉή»Υ ΐΒΡ±»άΐΫœ¥σΘ§
Υυ“‘≥Ϊ“ιΫώΚσΒΡΜΖΨ≥ΗΡ…Τ÷–―œΗώΩΊ÷ΤΙΛ≥ßΒΡΈέ»Ψ≈≈Ζ≈Θ§Ά§ ± –ΟώΕύ≥ΥΉχΙΪΙ≤Τϊ≥ΒΘ§Φθ…ΌΥΫΦ“≥Β≥ω––ΒΡ¥Έ ΐ
ΓΨΖ÷ΈωΓΩ
ΓΨΫβΈωΓΩΫβΘΚΘ®1Θ©ΗυΨίΧβ“βΘ§±Ψ¥ΈΒς≤ιΒΡΉή»Υ ΐΈΣ40Γ¬10%=400Θ®»ΥΘ©Θ§
Γύm=400ΓΝ20%=80Θ§n=400©¹Θ®80+40+120+60Θ©=100Θ§
‘ρ…»–ΈΆ≥ΦΤΆΦ÷–C―ΓœνΥυ’ΦΒΡΑΌΖ÷±»ΈΣ ![]() ΓΝ100%=25%Θ§
ΓΝ100%=25%Θ§
Υυ“‘¥πΑΗ «ΘΚ80Θ§100Θ§25%ΘΜ
ΓΨΩΦΒψΨΪΈωΓΩ’ΤΈ’Ά≥ΦΤ±μΚΆ…»–ΈΆ≥ΦΤΆΦ «Ϋβ¥π±ΨΧβΒΡΗυ±ΨΘ§–η“Σ÷ΣΒά÷ΤΉςΆ≥ΦΤ±μΒΡ≤Ϋ÷ηΘΚΘ®1Θ© ’Φ·’ϊάμ ΐΨίΘ°Θ®2Θ©»ΖΕ®Ά≥ΦΤ±μΒΡΗώ ΫΚΆάΗΡΩ ΐΝΩΘ§ΗυΨί÷Ϋ’≈¥σ–Γ÷Τ≥…±μΗώΘ°Θ®3Θ©Χν–¥άΗΡΩΓΔΗςœνΡΩΟϊ≥ΤΦΑ ΐΨίΘ°Θ®4Θ©ΦΤΥψΉήΦΤΚΆΚœΦΤ≤ΔΧν»κ±μ÷–Θ§“ΜΑψΉήΦΤΖ≈‘ΎΚαάΗΉνΉσΗώΘ§ΚœΦΤΖ≈‘Ύ ζάΗΉν…œΗώΘ°Θ®5Θ©–¥ΚΟ±μΗώΟϊ≥Τ≤Δ±ξΟς÷Τ±μ ±ΦδΘΜΡή«ε≥ΰΒΊ±μ Ψ≥ωΗς≤ΩΖ÷‘ΎΉήΧε÷–Υυ’ΦΒΡΑΌΖ÷±»Θ°ΒΪ «≤ΜΡή«ε≥ΰΒΊ±μ Ψ≥ωΟΩΗωœνΡΩΒΡΨΏΧε ΐΡΩ“‘ΦΑ ¬ΈοΒΡ±δΜ·«ιΩωΘ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
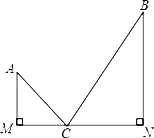
ΓΨΧβΡΩΓΩ»γΆΦΘΚ‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ADΓΈBCΘ§«“BC=12cmΘ§AD=18cmΘ§PΓΔQΖ÷±π¥”AΓΔCΆ§ ±≥ωΖΔΘ§P“‘2cm/sΒΡΥΌΕ»”…AœρD‘ΥΕ·Θ§Q“‘4cm/sΒΡΥΌΕ»”…CœρB‘ΥΕ·Θ§Έ Β±Εύ…ΌΟκ ±,÷±œΏQPΫΪΥΡ±Ώ–ΈABCDΫΊ≥ω“ΜΗωΤΫ––ΥΡ±Ώ–ΈΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘΚ“―÷ΣΘΚ![]() Θ§
Θ§![]() Θ§¥ΙΉψΖ÷±πΈΣ
Θ§¥ΙΉψΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() Θ§Βψ
Θ§Βψ![]() «
«![]() …œ Ι
…œ Ι![]() ΒΡ÷ΒΉν–ΓΒΡΒψΘ°»τ
ΒΡ÷ΒΉν–ΓΒΡΒψΘ°»τ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ________Θ°
________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΗω÷±ΝΔΒΡΜπ≤ώΚ–‘ΎΉάΟφ…œΒΙœ¬Θ§ΤτΒœ»ΥΟ«ΖΔœ÷ΝΥΙ¥Ι…Ε®άμΒΡ“Μ÷÷–¬ΒΡ―ι÷ΛΖΫΖ®.»γΆΦΘ§Μπ≤ώΚ–ΒΡ“ΜΗω≤ύΟφ![]() ΒΙœ¬ΒΫ
ΒΙœ¬ΒΫ![]() ΒΡΈΜ÷ΟΘ§Ν§Ϋ”
ΒΡΈΜ÷ΟΘ§Ν§Ϋ”![]() Θ§…η
Θ§…η![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Θ§«κάϊ”ΟΥΡ±Ώ–Έ
Θ§«κάϊ”ΟΥΡ±Ώ–Έ![]() ΒΡΟφΜΐ―ι÷ΛΙ¥Ι…Ε®άμ.
ΒΡΟφΜΐ―ι÷ΛΙ¥Ι…Ε®άμ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΝΫΧθ≥ΛΕ»ΨυΈΣ2ΒΡœΏΕΈ![]() ΚΆœΏΕΈ
ΚΆœΏΕΈ![]() ΜΞœύ÷ΊΚœΘ§ΫΪ
ΜΞœύ÷ΊΚœΘ§ΫΪ![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() œρΉσΤΫ“Τ
œρΉσΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΫΪ
ΗωΒΞΈΜ≥ΛΕ»Θ§ΫΪ![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() œρ”““≤ΤΫ“Τ
œρ”““≤ΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§Β±
ΗωΒΞΈΜ≥ΛΕ»Θ§Β±![]() ΓΔ
ΓΔ![]() «œΏΕΈ
«œΏΕΈ![]() ΒΡ»ΐΒ»Ζ÷Βψ ±Θ§‘ρ
ΒΡ»ΐΒ»Ζ÷Βψ ±Θ§‘ρ![]() ΒΡ÷ΒΈΣ________.
ΒΡ÷ΒΈΣ________.
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓœ1=Γœ3Θ§Γœ2+Γœ3=180Θ§«κΥΒΟςAB”κDEΤΫ––ΒΡάμ”…Θ°
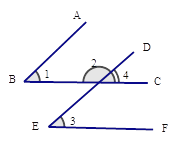
ΫβΘΚΫΪΓœ2ΒΡΝΎ≤ΙΫ«Φ«ΉςΓœ4Θ§‘ρ
Γœ2+Γœ4=180ΓψΘ® Θ©
“ρΈΣΓœ2+Γœ3=180ΓψΘ® Θ©
Υυ“‘Γœ3=Γœ4Θ® Θ©
“ρΈΣ______________Θ®“―÷ΣΘ©
Υυ“‘Γœ1=Γœ4Θ® Θ©
Υυ“‘AB//DEΘ® Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏABΓΈCDΘ§AEΤΫΖ÷ΓœCABΘ§AE”κCDœύΫΜ”ΎΒψEΘ§ΓœACD=40ΓψΘ§‘ρΓœDEA=Θ® Θ©
A.40Γψ
B.110Γψ
C.70Γψ
D.140Γψ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“ΜΥ“¬÷¥§ΈΜ”ΎΒΤΥΰPΒΡ±±ΤΪΕΪ60ΓψΖΫœρΘ§”κΒΤΥΰPΒΡΨύάκΈΣ30ΚΘάοΒΡA¥ΠΘ§¬÷¥§―Ί’ΐΡœΖΫœρΚΫ––“ΜΕΈ ±ΦδΚσΘ§ΒΫ¥οΈΜ”ΎΒΤΥΰPΒΡΡœΤΪΕΪ30ΓψΖΫœρ…œΒΡB¥ΠΘ§‘ρ¥Υ ±¬÷¥§Υυ‘ΎΈΜ÷ΟB¥Π”κΒΤΥΰP÷°ΦδΒΡΨύάκΈΣΘ® Θ©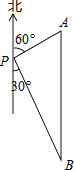
A.60ΚΘάο
B.45ΚΘάο
C.20 ![]() ΚΘάο
ΚΘάο
D.30 ![]() ΚΘάο
ΚΘάο
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ…œ”–ΗωΒψ![]() Θ§Βψ
Θ§Βψ![]() ΒΎ1¥Έœρ…œΧχΕ·1ΗωΒΞΈΜ÷ΝΒψ
ΒΎ1¥Έœρ…œΧχΕ·1ΗωΒΞΈΜ÷ΝΒψ![]() Θ§ΫτΫ”Ή≈ΒΎ2¥ΈœρΉσΧχΕ·2ΗωΒΞΈΜ÷ΝΒψ
Θ§ΫτΫ”Ή≈ΒΎ2¥ΈœρΉσΧχΕ·2ΗωΒΞΈΜ÷ΝΒψ![]() Θ§ΒΎ3¥Έœρ…œΧχΕ·1ΗωΒΞΈΜΘ§ΒΎ4¥Έœρ”“ΧχΕ·3ΗωΒΞΈΜΘ§ΒΎ5¥Έ”÷œρ…œΧχΕ·1ΗωΒΞΈΜΘ§ΒΎ6¥ΈœρΉσΧχΕ·4ΗωΒΞΈΜΘ§Γ≠Γ≠Θ§“ά¥ΥΙφ¬…ΧχΕ·œ¬»ΞΘ§ΒψPΒΎ200¥ΈΧχΕ·÷ΝΒψ
Θ§ΒΎ3¥Έœρ…œΧχΕ·1ΗωΒΞΈΜΘ§ΒΎ4¥Έœρ”“ΧχΕ·3ΗωΒΞΈΜΘ§ΒΎ5¥Έ”÷œρ…œΧχΕ·1ΗωΒΞΈΜΘ§ΒΎ6¥ΈœρΉσΧχΕ·4ΗωΒΞΈΜΘ§Γ≠Γ≠Θ§“ά¥ΥΙφ¬…ΧχΕ·œ¬»ΞΘ§ΒψPΒΎ200¥ΈΧχΕ·÷ΝΒψ![]() ΒΡΉχ±ξ «Θ® Θ©
ΒΡΉχ±ξ «Θ® Θ©

A. (51,100)B. (50,100)C. (-50,100)D. (-51,100)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com