
【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .

【答案】(1)①∠DBA=∠ECA,证明见解析;②80°;(2)50°或130°.
【解析】试题分析:(1)①根据同角的余角的相等即可说明∠DBA=∠ECA,根据四边形的内角和是360°,求得∠DHE的度数;
(2)分△ABC是锐角三角形,钝角三角形两种情况讨论求解即可.
(1)①∠DBA=∠ECA.
证明:∵BD、CE是△ABC的两条高,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠BAD=∠ECA+∠EAC=90°,
又∵∠BAD=∠EAC,
∴∠DBA=∠ECA;
②∵BD、CE是△ABC的两条高
∴∠HDA=∠HEA=90°
在四边形ADHE中,∠DAE+∠HDA+∠DHE+∠HEA=360°
又∵∠HDA=∠HEA=90°,∠DAE=∠BAC=100°
∴∠DHE=360°-90°-90°-100°=80°
(2)①△ABC是锐角三角形时,∠DHE=180°-50°=130°;
②△ABC是钝角三角形时,∠DHE=∠A=50°;
故答案为:50°或130°.


科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= ![]() ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( ) 
A.0个
B.1个
C..2个
D..3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B、C、D在数轴上的位置如图1所示,已知AB=3,BC=2,CD=4.
(1)若点C为原点,则点A表示的数是 ;
(2)若点A、B、C、D分别表示有理数a,b,c,d,则|a﹣c|+|d﹣b|﹣|a﹣d|= ;
(3)如图2,点P、Q分别从A、D两点同时出发,点P沿线段AB以每秒1个单位长度的速度向右运动,到达B点后立即按原速折返;点Q沿线段CD以每秒2个单位长度的速度向左运动,到达C点后立即按原速折返.当P、Q中的某点回到出发点时,两点同时停止运动.
①当点停止运动时,求点P、Q之间的距离;
②设运动时间为t(单位:秒),则t为何值时,PQ=5?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全国爱眼日是每年的6月6日,2013年世界爱眼日主题确定为“关爱青少年眼健康”,某中学为了解该校学生的视力情况,采用抽样调查的方式,从视力正常、轻度近视、中度近视、重度近视四个方面调查了若干名学生的视力情况,并根据调查结果制作了如下两幅统计图. 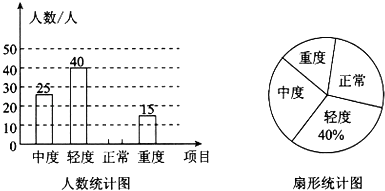
根据图中提供的信息解答下列问题:
(1)一共随机调查了多少人?
(2)补全人数统计图;
(3)若该校共有1500名学生,请你估计该校学生视力正常的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
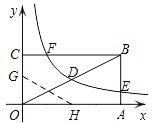
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求G点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,某省试行阶梯电价收费制,具体执行方案如下:
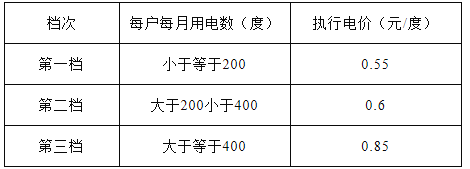
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).
某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com