
���� ��1�����M������Ϊ��m��$\frac{3}{m}$�������ݹ���ֵ�Ķ���ʽ�ɵó�����m��һԪ���η��̣��ⷽ�̼��ɵó�m��ֵ����m��ֵ���뵽��M�������м��ɵó����ۣ�
��2�����N������Ϊ��x��y�������ݹ���ֵ�Ķ���ʽ�ɷֶ��ҳ�y����x�ĺ�������ʽ������ͼ��������ε������ʽ���ɵó����ۣ�
��� �⣺��1�����M������Ϊ��m��$\frac{3}{m}$����
�ߡ�M��=4=|m|+|$\frac{3}{m}$|��
��m2-4m+3=0����m2+4m+3=0��
��ã�m1=1��m2=3��m3=-1��m4=-3��
���M������Ϊ��-3��-1������-1��-3������1��3���ͣ�3��1����
��2�����N��������x��y����
�ߡ�N��=3=|x|+|y|��
�������������ǣ�
��xy��0ʱ��x+y=3��x��y��Ϊ��������x+y=-3��x��y��Ϊ������
��xy��0ʱ��x-y=3��x��0��y��0������-x+y=3��x��0��y��0����
��xy=0ʱ��x=0��y=��3����y=0��x=��3��
����ͼ����ͼ��ʾ��
��A��0��3����B��3��0����C��0��-3����D��-3��0����
Χ��ͼ�ε����S=BD•AC=[3-��-3��]��[3-��-3��]=6��6=36��
���� ���⿼���˷���������ͼ���ϵ����������������Ĺؼ��ǣ���1���ҳ�����m��һԪ���η��̣���2���ֶ��ҳ�y����x�ĺ�����ϵʽ���������ڻ����⣬�ѶȲ������������Ŀʱ����ȷ�����ֵ�Ķ����Լ��ܹ���ȷ���ù���ֵ�Ķ���ʽ�ǹؼ���


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-1 | B�� | x=1 | C�� | x=-$\frac{1}{2}$ | D�� | x=��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڱ߳�Ϊ6��������ABCD�У�E�DZ�CD���е㣬����ADE��AE��������AFE���ӳ���BC�ڵ�G������AG����sin��BAG=$\frac{\sqrt{10}}{10}$��
��ͼ���ڱ߳�Ϊ6��������ABCD�У�E�DZ�CD���е㣬����ADE��AE��������AFE���ӳ���BC�ڵ�G������AG����sin��BAG=$\frac{\sqrt{10}}{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
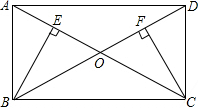 ��ͼ������ABCD�У�AC��BD���ڵ�O��BE��AC��CF��BD������ֱ�ΪE��F����֤��
��ͼ������ABCD�У�AC��BD���ڵ�O��BE��AC��CF��BD������ֱ�ΪE��F����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com