
分析 (1)设抛物线解析式为y=ax2,把A(4,-4)代入得到a=-$\frac{1}{4}$,直线l为y=kx-4-4k,由由$\left\{\begin{array}{l}{y=-\frac{1}{4}{x}^{2}}\\{y=kx-4-4k}\end{array}\right.$,消去y得到x2+4kx-16-16k=0,根据题意△=0,列出方程即可解决问题.
(2))①如图1中,作DM⊥OC于M,直线l交x轴于N.由△BCD~△ACB,得$\frac{BC}{AC}$=$\frac{CD}{BC}$,求出CD的长,再根据DM∥ON,得到$\frac{DM}{ON}$=$\frac{CD}{CN}$,求出DM得到点P横坐标,由此即可解决问题.
②不存在.过点P作y轴的平行线,交B′C于G,交AB于H,设P(m,-$\frac{1}{4}$m2),根据PG=2PH,列出方程,方程无解,说明这样的点P不存在.
解答 解:(1)由题意设抛物线解析式为y=ax2,把A(4,-4)代入得到a=-$\frac{1}{4}$,
∴抛物线的解析式为y=-$\frac{1}{4}$x2,
设直线l的解析式为y=kx+b,A(4,-4)代入得到,b=-4-4k,
∴直线l为y=kx-4-4k,
由$\left\{\begin{array}{l}{y=-\frac{1}{4}{x}^{2}}\\{y=kx-4-4k}\end{array}\right.$,消去y得到x2+4kx-16-16k=0,
由题意△=0,
∴16k2+64k+64=0,
∴k2+4k+4=0,
∴k=-2,
∴直线l的解析式为y=-2x+4.
(2)①如图1中,作DM⊥OC于M,直线l交x轴于N.
∵C(0,4),N(2,0),B(0,-1),
∴BC=5,ON=2,AC=4$\sqrt{5}$,CN=2$\sqrt{5}$,
∵△BCD~△ACB,
∴$\frac{BC}{AC}$=$\frac{CD}{BC}$,
∴$\frac{5}{4\sqrt{5}}$=$\frac{CD}{5}$,
∴CD=$\frac{5\sqrt{5}}{4}$,
∵DM∥ON,
∴$\frac{DM}{ON}$=$\frac{CD}{CN}$,
∴$\frac{DM}{2}$=$\frac{\frac{5\sqrt{5}}{4}}{2\sqrt{5}}$,
∴DM=$\frac{5}{4}$,
∴点P的横坐标为$\frac{5}{4}$,
∴x=$\frac{5}{4}$时,y=-$\frac{25}{64}$,
∴点P坐标($\frac{5}{4}$,-$\frac{25}{64}$).
②如图2中,不存在.
理由:过点P作y轴的平行线,交B′C于G,交AB于H,设P(m,-$\frac{1}{4}$m2).
∵S△B′CP=2S△ABP,
∴PG=2PH,
由题意B′(4,-1),
∵C(0,4),B(0,-1),A(4,-4),
∴直线AB的解析式为y=-$\frac{3}{4}$x-1,直线B′C的解析式为y=-$\frac{3}{4}$x+4,
∴G(m,-$\frac{3}{4}$m+4),H(m,-$\frac{3}{4}$m-1),
∴PG=-$\frac{3}{4}$m+4-(-$\frac{1}{4}$m2),PH=-$\frac{1}{4}$m2-(-$\frac{3}{4}$m-1),
∴-$\frac{3}{4}$m+4-(-$\frac{1}{4}$m2)=2[-$\frac{1}{4}$m2-(-$\frac{3}{4}$m-1)],
整理得3m2-9m+8=0,
∵△=92-4×3×8=-15<0,
∴方程无解,
∴不存在这样的点P使得S△B′CP=2S△ABP.
点评 本题考查二次函数综合题、一次函数的应用、旋转变换、相似三角形的判定和性质、平行线等分线段定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 月龄/月 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 体重/g | 3500 | 4200 | 4900 | 5600 | 6300 | 7000 | 7700 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
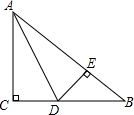 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且△ACD的周长为30,AD=13cm,则斜边AB长为17cm.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且△ACD的周长为30,AD=13cm,则斜边AB长为17cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com