
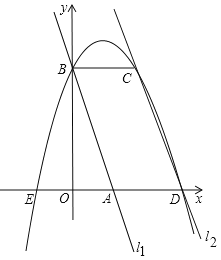
【题目】如图,在平面直角坐标系中两条直线为l1:y=–3x+3,l2:y=–3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a–b+c=0;
②2a+b+c=5;
③抛物线关于直线x=1对称;
④抛物线过点(b,c);
⑤S四边形ABCD=5;
其中正确的个数有( )
A. 5 B. 4 C. 3 D. 2
【答案】C
【解析】解:∵直线l1:y=﹣3x+3交x轴于点A,交y轴于点B,∴A(1,0),B(0,3),∵点A、E关于y轴对称,∴E(﹣1,0).
∵直线l2:y=﹣3x+9交x轴于点D,过点B作x轴的平行线交l2于点C,∴D(3,0),C点纵坐标与B点纵坐标相同都是3,把y=3代入y=﹣3x+9,得3=﹣3x+9,解得x=2,∴C(2,3).
∵抛物线![]() 过E、B、C三点,∴
过E、B、C三点,∴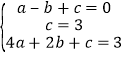 ,解得:
,解得: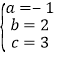 ,∴y=﹣x2+2x+3.
,∴y=﹣x2+2x+3.
①∵抛物线![]() 过E(﹣1,0),∴a﹣b+c=0,故①正确;
过E(﹣1,0),∴a﹣b+c=0,故①正确;
②∵a=﹣1,b=2,c=3,∴2a+b+c=﹣2+2+3=3≠5,故②错误;
③∵抛物线过B(0,3),C(2,3)两点,∴对称轴是直线x=1,∴抛物线关于直线x=1对称,故③正确;
④∵b=2,c=3,抛物线过C(2,3)点,∴抛物线过点(b,c),故④正确;
⑤∵直线l1∥l2,即AB∥CD,又BC∥AD,∴四边形ABCD是平行四边形,∴S四边形ABCD=BCOB=2×3=6≠5,故⑤错误.
综上可知,正确的结论有3个.
故选C.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度![]() 米,顶点
米,顶点![]() 距水面
距水面![]() 米(即
米(即![]() 米),小孔顶点
米),小孔顶点![]() 距水面
距水面![]() 米(即
米(即![]() 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度
米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度![]() 长为( )
长为( )
![]()

A. ![]() 米 B.
米 B. ![]() C.
C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),点P是等腰三角形ABC底边BC上的一动点,过点P作BC的垂线,交直线AB于点Q,交CA的延长线于点R.
(1)试猜想线段AR与AQ的长度之间存在怎样的数量关系?并证明你的猜想.
(2)如图(2),如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,其它条件不变,问(1)中所得的结论还成立吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y1=x﹣m+1和y2=![]() (n≠0)的图象交于P,Q两点.
(n≠0)的图象交于P,Q两点.
(1)若y1的图象过(n,0),且m+n=3,求y2的函数表达式:
(2)若P,Q关于原点成中心对称.
①求m的值;
②当x>2时,对于满足条件0<n<n0的一切n总有y1>y2,求n0的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件:______ .使得加上这个条件后能够推出AB=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)某数学兴趣小组想测量商丘电视台电视塔的高度,如图,该小组在商丘电视塔BC前一座楼房楼顶A处所观测到电视塔最高点B的仰角为65°,电视塔最低点C的仰角为30°,楼顶A与电视塔的水平距离AD为90米,求商丘电视塔BC的高度.(结果精确到1米,参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com