
【题目】如图,AB是⊙O的一条弦,且AB= ![]() .点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA. 
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为 ![]() ,直接写出∠BAF的度数.
,直接写出∠BAF的度数.
【答案】
(1)解:∵OC⊥AB,AB= ![]() ,
,
∴AD=DB=2 ![]() ,
,
∵∠E=30°,
∴∠AOD=60°,∠OAB=30°,
∴OA= ![]() =4
=4
(2)解:如图,作OH⊥AF于H,
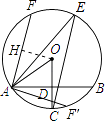
∵OA=4,OH=2 ![]() ,
,
∴∠OAF=45°,
∴∠BAF=∠OAF+∠OAB=75°,
则∠BAF′=∠OAF′﹣∠OAB=15°,
∴∠BAF的度数是75°或15°.
【解析】(1)根据垂径定理求出AD的长,根据圆周角定理求出∠AOD的度数,运用正弦的定义解答即可;(2)作OH⊥AF于H,根据勾股定理和等腰直角三角形的性质求出∠OAF的度数,分情况计算即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数为( )
①﹣a一定是负数;②一个有理数不是整数就是分数;③任何一个有理数的平方都是正数;④倒数等于它本身的数是±1;⑤绝对值等于它本身的数是0;⑥任何一个有理数的绝对值都是正数
A. 0 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年李明家买了一辆轿车,他连续记录了一周中每天行驶的路程(如下表),以50km为标准,多于50km的记“+”,不足50km的记“-”,刚好506m的记“0”.
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 | |
路程(km) | -6 | 0 | -12 | 7 | -9 | +15 | +12 |
(1)请你求出李明家轿车一周中平均每天行驶多少千米?
(2)如果每行驶100km需要汽油8升,汽油价格6.85元/升,请计算李明家轿车一个月(按30天计算)的汽油费是多少元(精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=4,点O是线段AB上的点,点C,D是线段OA,OB的中点,小明很轻松地求得CD=2.
![]()
(1)小明在反思过程中突发奇想:若点O运动到线段AB的延长线上,则原有的结论“CD=2”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
(2)当点O运动到直线AB外时,结论“CD=2”是否还成立?请利用刻度尺验证你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=kx+b和函数y=ax+m的图像如图所示,求下列不等式(组)的解集
(1) kx+b <ax+m的解集是
(2)![]() 的解集是
的解集是
(3)![]() 的解集是
的解集是
(4)![]() 的解集是
的解集是
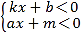
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(3-k)x-2k2+18.
(1)当k为何值时,它的图象经过原点?
(2)当k为何值时,它的图象经过点(0,-2)?
(3)当k为何值时,它的图象平行于直线y=-x?
(4)当k为何值时,y随x增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S=![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com