
【题目】如图, ![]() 是边长为
是边长为![]() 的等边三角形,边
的等边三角形,边![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将
出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将![]() 绕点C逆时针方向旋转60°得到
绕点C逆时针方向旋转60°得到![]() ,连接DE.
,连接DE.
(1)如图1,求证: ![]() 是等边三角形;
是等边三角形;
(2)如图2,当6<t<10时,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
(3)当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.

【答案】(1)证明见解析;(2)存在, DE=2![]() cm;(3)存在,当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
cm;(3)存在,当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
【解析】试题分析:
(1)由旋转的性质结合△ABC是等边三角形可得∠DCB=60°,CD=CE,从而可得△CDE是等边三角形;
(2)由(1)可知△CDE是等边三角形,由此可得DE=CD,因此当CD⊥AB时,CD最短,则DE最短,结合△ABC是等边三角形,AC=4即可求得此时DE=CD=![]() ;
;
(3)由题意需分0≤t<6,6<t<10和t>10三种情况讨论,①当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,由此可知:此时若△DBE是直角三角形,则∠BED=90°;②当6<t<10s时,由性质的性质可知∠DBE=120°>90°,由此可知:此时△DBE不可能是直角三角形;③当t>10s时,由旋转的性质可知,∠DBE=60°,结合∠CDE=60°可得∠BDE=∠CDE+∠BDC=60°+∠BDC>60°,由此可得∠BED<60°,由此可知此时若△BDE是直角三角形,则只能是∠BDE=90°;这样结合已知条件即可分情况求出对应的t的值了.
试题解析:
(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
(2)存在,当6<t<10时,
由(1)知,△CDE是等边三角形,
∴DE=CD,
由垂线段最短可知,当CD⊥AB时,CD最小,
此时∠ADC=90°,又∵∠ACD=60°,
∴∠ACD=30°,
∴ AD=![]() AC=2,
AC=2,
∴ CD=![]() ,
,
∴ DE=2![]() (cm);
(cm);

(3)存在,理由如下:
①当0s≤t<6s时,由旋转可知,∠ABE=60°,∠BDE<60°,
∴此时若△DBE是直角三角形,则∠BED=90°,
由(1)可知,△CDE是等边三角形,
∴∠DEC=60°,
∴∠CEB=∠BED-∠DEC=30°,
∴∠CDA=∠CEB=30°,
∵∠CAB=60°,
∴∠ACD=∠ADC=30°,
∴DA=CA=4,
∴OD=OA﹣DA=6﹣4=2,
∴t=2÷1=2(s);
②当6s<t<10s时,由性质的性质可知∠DBE=120°>90°,
∴此时△DBE不可能是直角三角形;
③当t>10s时,由旋转的性质可知,∠DBE=60°,
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4,
∴OD=14cm,
∴t=14÷1=14(s);
综上所述:当t=2s或14s时,以D、E、B为顶点的三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=![]() , FC=FN,EN=
, FC=FN,EN=![]() , 则EF=
, 则EF= 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在课堂上出了一个问题:若点A(﹣2,y1),B(1,y2)和C(4,y3)都在反比例函数y=![]() 的图象上,比较y1 , y2 , y3的大小.
的图象上,比较y1 , y2 , y3的大小.
小明是这样思考的:当k<0时,反比例函数的图象是y随x的增大而增大的,并且﹣2<1<4,所以y1<y2<y3 .
你认为小明的思考 (填“正确”和“不正确”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(﹣1,t),B(3,t),与y轴交于点C(0,﹣1).一次函数y=x+n的图象经过抛物线的顶点D.
(1)求抛物线的表达式;
(2)求一次函数y=x+n的表达式;
(3)将直线l:y=mx+n绕其与y轴的交点E旋转,使当﹣1≤x≤1时,直线l总位于抛物线的下方,请结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
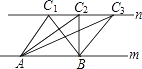
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF ;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)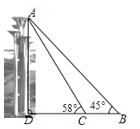
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
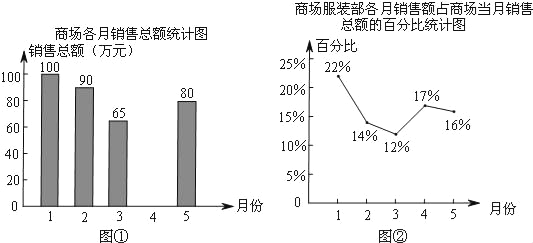
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com