
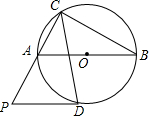
 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的角平分线交⊙O于D,过D作⊙O的切线交CA的延长线于P.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的角平分线交⊙O于D,过D作⊙O的切线交CA的延长线于P.分析 (1)根据圆周角定理即可证得∠BAD=∠ABD,∠ADB=90°,从而证得△ADB是等腰直角三角形,解直角三角形即可证得结论;
(2)设AC=x,根据sin∠B=$\frac{3}{5}$得出AB=$\frac{5}{3}$x,进而得出AD=$\frac{\sqrt{2}}{2}$AB=$\frac{5\sqrt{2}}{6}$x,作AE⊥CD,得出△ACE为等腰直角三角形,从而求得AE=CE=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$x,根据勾股定理求得ED,即可求得CD,然后证得△PDA∽△PCD,根据相似三角形的性质即可求得.
解答 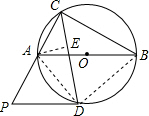 (1)证明:连接AD,BD,
(1)证明:连接AD,BD,
∵∠ACB的角平分线交⊙O于D,
∴∠ACD=∠BCD,
∵∠BAD=∠BCD,∠ABD=∠ACD,
∴∠BAD=∠ABD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB=45°,
∴AD=$\frac{\sqrt{2}}{2}$AB,
∴AB=$\sqrt{2}$AD;
(2)解:在Rt△ACB中,∵sin∠B=$\frac{3}{5}$,
∴$\frac{AC}{AB}$=$\frac{3}{5}$,
设AC=x,
∴AB=$\frac{5}{3}$x,
∵△DAB为等腰直角三角形,
∴AD=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×$\frac{5}{3}$x=$\frac{5\sqrt{2}}{6}$x,
作AE⊥CD,
∴△ACE为等腰直角三角形,
∴AE=CE=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$x,
在Rt△AED中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{(\frac{5\sqrt{2}}{6}x)^{2}-(\frac{\sqrt{2}}{2}x)^{2}}$=$\frac{2\sqrt{2}}{3}$x,
∴CD=CE+DE=$\frac{\sqrt{2}}{2}$x+$\frac{2\sqrt{2}}{3}$x=$\frac{7\sqrt{2}}{6}$x,
∵∠PDA=∠PCD,∠P=∠P,
∴△PDA∽△PCD,
∴$\frac{PA}{PD}$=$\frac{AD}{CD}$=$\frac{\frac{5\sqrt{2}}{6}x}{\frac{7\sqrt{2}}{6}x}$=$\frac{5}{7}$.
点评 此题考查了切线的性质和圆周角定理定理、等腰直角三角形的性质和三角形相似的判定与性质等知识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
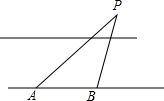 在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)
在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:解答题
某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、 D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
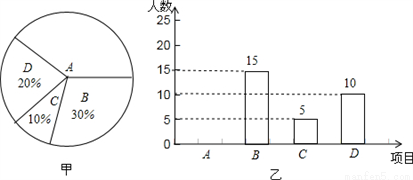
(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
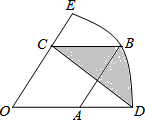 如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.
如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( ).
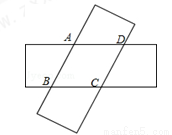
A. 15 B. 16 C. 19 D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com