
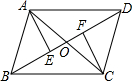
 如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对.
如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对. 分析 根据平行四边形的性质,即可得知对比相等且平行,再根据平行找出相等的内错角,即可用全等三角形的判定定理SAS证出△ABD≌△CDB、△ABC≌△DCA;由对角线互相平分及对顶角相等能得出“AO=CO,BO=DO,∠AOB=∠COD,∠AOD=∠COB”,用全等三角形的判定定理SSS可证出△AOD≌△COB、△AOB≌△COD;由“AE⊥BD于E,AF⊥BD于F”可得出AE∥CF,即得出∠EAO=∠FCO,用全等三角形的判定定理ASA即可证出△EAO≌△FCO,同理亦可证出△ABE≌△CDF.故图中的全等三角形有6对.
解答 解:∵四边形为平行四边形,
∴AD=BC,AB=CD,AD∥BC,AB∥CD,
∴∠DBC=∠BDA,∠ABD=∠CDB,∠BAC=∠DCA,∠DAC=∠BCA.
在△ABD和△CDB中,
$\left\{\begin{array}{l}{AD=CB}\\{∠ABD=∠CDB}\\{BD=DB}\end{array}\right.$,
∴△ABD≌△CDB(SAS);
在△ABC和△DCA中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAC=∠DCA}\\{AC=CA}\end{array}\right.$,
∴△ABC≌△DCA(SAS);
∵AC与BD相交于点O,
∴AO=CO,BO=DO,∠AOB=∠COD,∠AOD=∠COB.
在△AOD和△COB中,
$\left\{\begin{array}{l}{AD=CB}\\{AO=CO}\\{DO=BO}\end{array}\right.$,
∴△AOD≌△COB(SSS);
在△AOB和△COD中,
$\left\{\begin{array}{l}{AB=CD}\\{AO=CO}\\{BO=DO}\end{array}\right.$,
∴△AOB≌△COD(SSS);
∵AE⊥BD于E,AF⊥BD于F,
∴AE∥CF,
∴∠EAO=∠FCO.
在△EAO和△FCO中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△EAO≌△FCO(ASA).
同理可得出△ABE≌△CDF.
综上可知有6对全等的三角形.
故答案为:6.
点评 本题考查了全等三角形的判定,解题的关键根据平行四边形的性质以及平行线的性质得出相等的边角关系.本题属于基础题,难度不大,在做该题时,由四边形为平行四边形可直接找出“△ABD≌△CDB,△ABC≌△DCA,△AOD≌△COB,△AOB≌△COD”这4对全等的三角形,再结合垂直于同一条直线的两直线平行即能找出另外两对全等的三角形.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
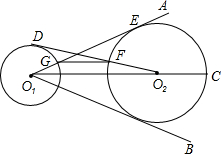 如图,⊙O1与⊙O2外离,O1C是∠AO1B的角平分线,O1C经过点O2,O1A切⊙O2于点E,交⊙O1于点G.
如图,⊙O1与⊙O2外离,O1C是∠AO1B的角平分线,O1C经过点O2,O1A切⊙O2于点E,交⊙O1于点G.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:判断题
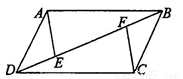
如图,已知四边形 为平行四边形,
为平行四边形, 、
、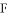 为对角线
为对角线 上的两点,且
上的两点,且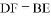 ,连接
,连接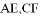 。求证:(1)
。求证:(1)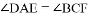 。(2)连接AC交于BD点O,求证AC,EF互相平分
。(2)连接AC交于BD点O,求证AC,EF互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
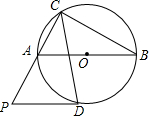 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的角平分线交⊙O于D,过D作⊙O的切线交CA的延长线于P.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的角平分线交⊙O于D,过D作⊙O的切线交CA的延长线于P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
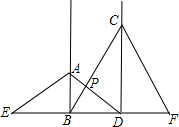 如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$)2 | B. | ($\frac{3}{4}$)-2 | C. | ($\frac{6}{5}$)2 | D. | ($\frac{6}{7}$)0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
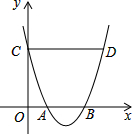 如图,对称轴平行于y轴的抛物线与x轴交于点A、B,与y轴交于点C,过C作CD∥x轴,与抛物线交于点D.若OA=1,CD=4,则线段AB的长为2.
如图,对称轴平行于y轴的抛物线与x轴交于点A、B,与y轴交于点C,过C作CD∥x轴,与抛物线交于点D.若OA=1,CD=4,则线段AB的长为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com