练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．计算：（$\sqrt{5}$-2）（$\sqrt{5}$+2）+$\sqrt{12}$-（$\frac{1}{3}$）-1．

    分析 分别根据数的开方法则及0指数幂的运算法则计算出各数，再按照有理数混合运算的顺序进行计算即可．

    解答 解：原式=5-4+2$\sqrt{3}$-3
    =2$\sqrt{3}$-2．

    点评 本题考查的是实数的运算，熟知数的开方法则及0指数幂的运算法则是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．如图，在?ABCD中，AC与BD相交于点O，AE⊥BD于E，AF⊥BD于F，则图中的全等三角形共有6对．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示，那么这个几何体表面积是22cm2，体积是5cm3．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷（解析版） 题型：单选题

    如图，由两个长为9，宽为3的全等矩形叠合而得到四边形ABCD，则四边形ABCD面积的最大值是（ ）．

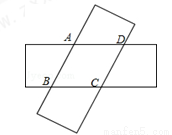
    A. 15 B. 16 C. 19 D. 20

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

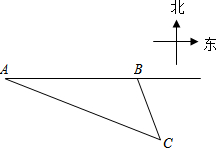    15．如图，我渔政船在东海海面上自西向东匀速巡航，在A地观测到某海岛C在东偏南21.3°方向上．若渔政船继续向东航行60海里到达B处，此时观测到海岛C在东偏南63.5°方向上．之后，渔政船再向东航多少海里，离海岛C的距离最近？
    （参考数据：sin21.3°≈$\frac{9}{25}$，tan21.3°$≈\frac{2}{5}$，sin63.5°$≈\frac{9}{10}$，tan63.5°≈2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．已知抛物线p：y=ax2+bx+c的顶点为C，与x轴相交于A、B两点（点A在点B的左侧），点C关于x轴的对称点为C′，我们称以A为顶点且过点C′，对称轴与y轴平行的抛物线为抛物线p的“关联”抛物线，直线AC′为抛物线p的“关联”直线．若一条抛物线的“关联”抛物线和“关联”直线分别是y=x2+2x+1和y=2x+2，则这条抛物线的解析式为y=x2-2x-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．若方程组$\left\{\begin{array}{l}{2a-3b=13}\\{3a+5b=30}\end{array}\right.$的解是$\left\{\begin{array}{l}{a=8.3}\\{b=1.2}\end{array}\right.$，则方程组$\left\{\begin{array}{l}{2（x+2）-3（y-1）=13}\\{3（x+2）+5（y-1）=30}\end{array}\right.$的解是（　　）
    A．$\left\{\begin{array}{l}{x=8.3}\\{y=1.2}\end{array}\right.$B．$\left\{\begin{array}{l}{x=10.3}\\{y=1.2}\end{array}\right.$C．$\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$D．$\left\{\begin{array}{l}{x=10.3}\\{y=0.2}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

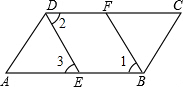    9．如图，∠ABC=∠ADC，BF、DE分别平分∠ABC与∠ADC，DE∥FB．求证：AB∥DC．
    请根据条件进行推理，得出结论，并在括号内注明理由．
    证明：∵BF、DE分别平分∠ABC与∠ADC，
    ∴∠1=$\frac{1}{2}$∠ABC，∠2=$\frac{1}{2}$∠ADC．（角平分线定义）
    ∵∠ABC=∠ADC，
    ∴∠1=∠2．
    ∵DE∥FB
    ∴∠1=∠3，（两直线平行，同位角相等）
    ∴∠2=∠3．（等量代换）
    ∴AB∥CD．（内错角相等，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

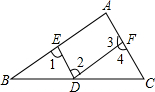    10．如图，下列条件：①∠1=∠2；②∠A=∠4；③∠1=∠4；④∠A+∠3=180°；⑤∠C=∠BDE，其中能判定AB∥DF的有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    同步练习册答案