
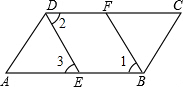
 ��ͼ����ABC=��ADC��BF��DE�ֱ�ƽ�֡�ABC���ADC��DE��FB����֤��AB��DC��
��ͼ����ABC=��ADC��BF��DE�ֱ�ƽ�֡�ABC���ADC��DE��FB����֤��AB��DC������ �ɽ�ƽ���ߵĶ���ó���1=$\frac{1}{2}$��ABC����2=$\frac{1}{2}$��ADC��֤����1=��2����ƽ���ߵ����ʵó���1=��3��֤����2=��3���ó�AB��CD���ɣ�
��� ֤������BF��DE�ֱ�ƽ�֡�ABC���ADC��
���1=$\frac{1}{2}$��ABC����2=$\frac{1}{2}$��ADC������ƽ���߶��壩
�ߡ�ABC=��ADC��
���1=��2��
��DE��FB
���1=��3������ֱ��ƽ�У�ͬλ����ȣ�
���2=��3��������������
��AB��CD�����ڴ�����ȣ���ֱ��ƽ�У�
�ʴ�Ϊ����ƽ���ߣ���1=��2����ֱ��ƽ�У�ͬλ����ȣ���3���ڴ�����ȣ���ֱ��ƽ�У�
���� ���⿼����ƽ���ߵ��ж������ʣ����ƽ���ߵ��ж��������ǽ������Ĺؼ���


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
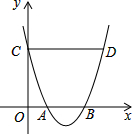 ��ͼ���Գ���ƽ����y�����������x�ύ�ڵ�A��B����y�ύ�ڵ�C����C��CD��x�ᣬ�������߽��ڵ�D����OA=1��CD=4�����߶�AB�ij�Ϊ2��
��ͼ���Գ���ƽ����y�����������x�ύ�ڵ�A��B����y�ύ�ڵ�C����C��CD��x�ᣬ�������߽��ڵ�D����OA=1��CD=4�����߶�AB�ij�Ϊ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
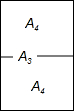 ��ӡֽ���ͺ���A0��A1��A2��A3��A4�ȣ�����֮�����������һ�ֹ�ϵ��������ijһ�ͺţ���A3���ĸ�ӡֽ�ϳ��ߵ��е���ۺ��ܵõ�������һ�ͺţ�A4���ĸ�ӡֽ���ҵõ����������ζ���ԭ���ľ������ƣ���ͼ������ô��Щ�ͺŵĸ�ӡֽ�ij���֮��Ϊ��������
��ӡֽ���ͺ���A0��A1��A2��A3��A4�ȣ�����֮�����������һ�ֹ�ϵ��������ijһ�ͺţ���A3���ĸ�ӡֽ�ϳ��ߵ��е���ۺ��ܵõ�������һ�ͺţ�A4���ĸ�ӡֽ���ҵõ����������ζ���ԭ���ľ������ƣ���ͼ������ô��Щ�ͺŵĸ�ӡֽ�ij���֮��Ϊ��������| A�� | 2��1 | B�� | $\sqrt{2}$��1 | C�� | $\sqrt{3}$��1 | D�� | 3��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=ax2+bx-4a����A��-1��0����C��0��4�����㣬��x�ύ����һ��B��
��ͼ��������y=ax2+bx-4a����A��-1��0����C��0��4�����㣬��x�ύ����һ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪���κ���y=ax2+bx+c��a��0���Ķ��������ǣ�-1��-5.2��������ͼ����ͼ������ͼ���֪����x��һԪ���η���ax2+bx+c=0���������ֱ���x1��x2����x1=1.3����x2��ֵΪ��������
��֪���κ���y=ax2+bx+c��a��0���Ķ��������ǣ�-1��-5.2��������ͼ����ͼ������ͼ���֪����x��һԪ���η���ax2+bx+c=0���������ֱ���x1��x2����x1=1.3����x2��ֵΪ��������| A�� | -1.3 | B�� | -2.3 | C�� | -0.3 | D�� | -3.3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
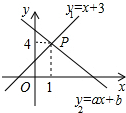 ��ͼ��һ�κ���y1=x+3��y2=ax+b��ͼ���ཻ�ڵ�P��1��4���������x�IJ���ʽx+3��ax+b�Ľ⼯�ǣ�������
��ͼ��һ�κ���y1=x+3��y2=ax+b��ͼ���ཻ�ڵ�P��1��4���������x�IJ���ʽx+3��ax+b�Ľ⼯�ǣ�������| A�� | x��4 | B�� | x��4 | C�� | x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com