
分析 (1)利用完全平方公式的结构特征判断即可;
(2)利用完全平方公式的结构特征求出m与n的值,即可确定出原式的值;
(3)利用完全平方公式的结构特征判断即可.
解答 解:(1)①a6=(a2)3;②a2-ab+b2,不是完全平方式;③4a2+2ab+$\frac{1}{4}$b2=(2a+$\frac{1}{2}$b)2;④x2+4xy+4y2=(x+2y)2;⑤a2+a+0.25=(a+$\frac{1}{2}$)2;⑥x2-6x-9,不是完全平方式
各式中完全平方式的编号有①③④⑤;
故答案为:①③④⑤;
(2)∵x2+4xy+my2和x2-nxy+$\frac{1}{4}$y2都是完全平方式,
∴x2+4xy+my2=(x+$\sqrt{m}$y)2,x2-nxy+$\frac{1}{4}$y2=(x±$\frac{1}{2}$y)2,
∴m=4,n=±1,
当n=1时,原式=$\frac{1}{3}$;当n=-1时,原式=$\frac{1}{5}$;
(3)单项式可以为-1,-9x2,6x,-6x或$\frac{81}{4}$x4.
点评 此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.


科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( ).
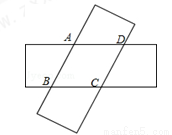
A. 15 B. 16 C. 19 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
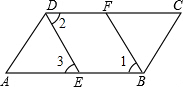 如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.
如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
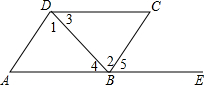 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠A+∠ABC=180° | C. | ∠A=∠5 | D. | ∠3=∠4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
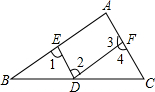 如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )
如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com