
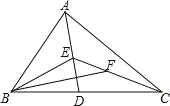
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

【答案】①②③④
【解析】①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
②正确;
③∠ABD=90°-∠BAC,
∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC,
∵∠CBE=90°-∠C,
∴∠DBE=∠BAC-∠C,
由①得,∠DBE=∠F,
∴∠F=∠BAC-∠C,
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠BGH=∠ABE,
∴∠BGH=∠ABE+∠C,
④正确,
故答案为:①②③④.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 ![]() 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 ![]() 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,已知点 D,E,F 分别是 BC,AD,CE 边上的中点,且 S△ABC=4cm2 则 S△BEF 的值为( )
A. 2cm2 B. 1cm2 C. 0.5cm2 D. 0.25cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
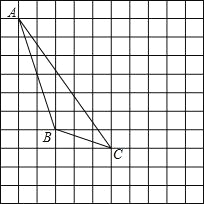
【题目】如图,每个小正方形的边长为 1 个单位,每个小方格的顶点叫格点.
(1)画出△ABC 的 AB 边上的中线 CD;
(2)画出△ABC 向右平移 4 个单位后得到的△A1B1C1;
(3)图中 AC 与 A1C1 的关系是: ;
(4)图中△ABC 的面积是 ;
(5)能使△BCE 面积为 3 的格点 E 有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com