
ЁОЬтФПЁПвбжЊЪ§жсЩЯШ§ЕуMЃЌOЃЌNЖдгІЕФЪ§ЗжБ№ЮЊЃ1ЃЌ0ЃЌ3ЃЌЕуPЮЊЪ§жсЩЯШЮвтвЛЕуЃЌЦфЖдгІЕФЪ§ЮЊxЃЎ
![]()
ЃЈ1ЃЉMNЕФГЄЮЊ ЃЛ
ЃЈ2ЃЉШчЙћЕуPЕНЕуMЁЂЕуNЕФОрРыЯрЕШЃЌФЧУДxЕФжЕЪЧ ЃЛ
ЃЈ3ЃЉЪ§жсЩЯЪЧЗёДцдкЕуPЃЌЪЙЕуPЕНЕуMЁЂЕуNЕФОрРыжЎКЭЪЧ8ЃПШєДцдкЃЌжБНгаДГіxЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉШчЙћЕуPвдУПЗжжг1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуOЯђзѓдЫЖЏЃЌЭЌЪБЕуMКЭЕуNЗжБ№вдУПЗжжг2ИіЕЅЮЛГЄЖШКЭУПЗжжг3ИіЕЅЮЛГЄЖШЕФЫйЖШвВЯђзѓдЫЖЏЃЎЩшtЗжжгЪБЕуPЕНЕуMЁЂЕуNЕФОрРыЯрЕШЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ4ЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉЃ3Лђ5ЃЛЃЈ4ЃЉtЕФжЕЮЊ![]() Лђ4ЃЎ
Лђ4ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЪ§жсЩЯСНЕужЎМфЕФОрРыЧѓЗЈМДПЩЕУЃЛ
ЃЈ2ЃЉИљОнШ§ЕуMЃЌNЖдгІЕФЪ§ЃЌЕУГіNMЕФжаЕуЮЊЃКx=ЃЈ-1+3ЃЉЁТ2ЧѓГіМДПЩЃЛ
ЃЈ3ЃЉИљОнPЕудкNЕугвВрЛђдкMЕузѓВрЗжБ№ЧѓГіМДПЩЃЛ
ЃЈ4ЃЉЩшОЙ§tУыЕуPЕНЕуMЁЂЕуNЕФОрРыЯрЕШЃЌдђЕуPЖдгІЕФЪ§ЪЧ-tЃЌЕуMЖдгІЕФЪ§ЪЧ-1 - 2tЃЌЕуNЖдгІЕФЪ§ЪЧ3 - 3tЃЎЃЌИљОнPM=PNНЈСЂЗНГЬЃЌЧѓНтМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉMNЕФГЄЮЊЃК|3-ЃЈ-1ЃЉ|=4ЃЌ
ЙЪД№АИЮЊЃК4ЃЛ
ЃЈ2ЃЉx=ЃЈ-1+3ЃЉЁТ2=1ЃЌ
ЙЪД№АИЮЊЃК1ЃЛ
ЃЈ3ЃЉЕБЕуPдкMЕузѓВрЪБЃЌдђгаЃЈ3-xЃЉ+(-1-x)=8ЃЌНтЕУЃКx=-3ЃЌ
ЕБЕуPдкNЕугвВрЪЧЪБЃЌдђгаЃЈx-3ЃЉ+[x-ЃЈ-1ЃЉ]=8ЃЌНтЕУЃКx=5ЃЌ
злЩЯЃЌxЕФжЕЪЧ-3Лђ5ЃЛ
ЃЈ4ЃЉЩшдЫЖЏtЗжжгЪБЃЌЕуPЕНЕуMЃЌЕуNЕФОрРыЯрЕШЃЌМДPM = PNЃЌ
ЕуPЖдгІЕФЪ§ЪЧ-tЃЌЕуMЖдгІЕФЪ§ЪЧ-1 - 2tЃЌЕуNЖдгІЕФЪ§ЪЧ3 - 3tЃЌ
ЂйЕБЕуMКЭЕуNдкЕуPЭЌВрЪБЃЌЕуMКЭЕуNжиКЯЃЌЫљвд-1 - 2t = 3 - 3tЃЌНтЕУt = 4ЃЌЗћКЯЬтвтЃЛ
ЂкЕБЕуMКЭЕуNдкЕуPвьВрЪБЃЌЕуMЮЛгкЕуPЕФзѓВрЃЌЕуNЮЛгкЕуPЕФгвВрЃЈвђЮЊШ§ИіЕуЖМЯђзѓдЫЖЏЃЌГіЗЂЪБЕуMдкЕуPзѓВрЃЌЧвЕуMдЫЖЏЕФЫйЖШДѓгкЕуPЕФЫйЖШЃЌЫљвдЕуMгРдЖЮЛгкЕуPЕФзѓВрЃЉЃЌЙЪPM = -t -ЃЈ-1 - 2tЃЉ= t + 1ЃЌPN=ЃЈ3 - 3tЃЉ-ЃЈ-tЃЉ= 3 - 2tЃЌ
Ыљвдt + 1 = 3 - 2tЃЌНтЕУt =![]() ЃЌЗћКЯЬтвтЃЌ
ЃЌЗћКЯЬтвтЃЌ
злЩЯЫљЪіЃЌtЕФжЕЮЊ![]() Лђ4ЃЎ
Лђ4ЃЎ


 ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЕудкжБЯпy=-x+1ЩЯЕФЪЧ ЃЈ ЃЉ
A. ЃЈ2ЃЌ-1ЃЉ B. ЃЈ3ЃЌ3ЃЉ C. ЃЈ4ЃЌ1ЃЉ D. ЃЈ1ЃЌ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнСЫНтЃЌИіЬхЗўзАЯњЪлвЊИпГіНјМлЕФ20%ЗНПЩгЏРћЃЌвЛЯњЪлРЯАхвдИпГіНјМлЕФ60%БъМлЃЌШчЙћвЛМўЗўзАБъМл240дЊЃЌФЧУДЃК
ЃЈ1ЃЉНјМлЪЧЖрЩйдЊЃПЃЈ2ЃЉзюЕЭЪлМлЖрЩйдЊЪБЃЌЯњЪлРЯАхЗНПЩгЏРћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбЖўДЮКЏЪ§yЃНЉЃЈx+1ЃЉ2Љ3ЕФЭМЯѓбизХxжсЗелКѓЃЌЕУЕНЕФЖўДЮКЏЪ§гаЃЈЁЁЁЁЃЉ
A.зюДѓжЕyЃН3B.зюДѓжЕyЃНЉ3C.зюаЁжЕyЃН3D.зюаЁжЕyЃНЉ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћжЛгУвЛжже§ЖрБпаЮзіЦНУцУмЦЬЃЌЖјЧвдкУПвЛИіе§ЖрБпаЮЕФУПвЛИіЖЅЕужмЮЇЖМга6Иіе§ЖрБпаЮЃЌдђИУе§ЖрБпаЮЕФУПИіФкНЧЖШЪ§ЮЊ______ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОчдКРя5ХХ2КХПЩвдгУ(5,2)БэЪО,ФЧУД3ХХ7КХПЩвдгУ________БэЪО.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЬтвтНтД№
ЃЈ1ЃЉвбжЊx= ![]() +1ЃЌy=
+1ЃЌy= ![]() Љ1ЃЌЧѓЯТСаИїЪНЕФжЕЃЎ Ђйx2+2xy+y2
Љ1ЃЌЧѓЯТСаИїЪНЕФжЕЃЎ Ђйx2+2xy+y2
Ђкx2Љy2
ЃЈ2ЃЉЯШЛЏМђЃЌдйЧѓжЕЃК ![]() ЁТЃЈ
ЁТЃЈ ![]() ЉaЃЉЃЌЦфжаa=
ЉaЃЉЃЌЦфжаa= ![]() Љ2ЃЎ
Љ2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
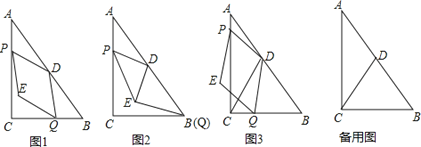
ЁОЬтФПЁПШчЭМ1ЃЌRtЁїABCжаЃЌЁЯACB=RtЁЯЃЌAC=8ЃЌBC=6ЃЌЕуDЮЊABЕФжаЕуЃЌЖЏЕуPДгЕуAГіЗЂЃЌбиACЗНЯђвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђжеЕуCдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШЯШбиCBЗНЯђдЫЖЏЕНЕуBЃЌдйбиBAЗНЯђЯђжеЕуAдЫЖЏЃЌвдDPЃЌDQЮЊСкБпЙЙдьPEQDЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉЕБt=2ЪБЃЌЧѓPDЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуQдЫЖЏжСЕуBЪБЃЌСЌНсDEЃЌЧѓжЄЃКDEЁЮAP.
ЃЈ3ЃЉШчЭМ3ЃЌСЌНсCDЃЎ
ЂйЕБЕуEЧЁКУТфдкЁїACDЕФБпЩЯЪБЃЌЧѓЫљгаТњзувЊЧѓЕФtжЕЃЛ
ЂкМЧдЫЖЏЙ§ГЬжаPEQDЕФУцЛ§ЮЊSЃЌPEQDгыЁїACDЕФжиЕўВПЗжУцЛ§ЮЊS1ЃЌЕБ![]() ЃМ
ЃМ![]() ЪБЃЌЧыжБНгаДГіtЕФШЁжЕЗЖЮЇЪЧ ______ ЃЎ
ЪБЃЌЧыжБНгаДГіtЕФШЁжЕЗЖЮЇЪЧ ______ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com