
【题目】某城市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计费;月用水量超过20m3时,超过部分按2.6元/m3计费.设每户家庭的月用水量为xm3时,应交水费y元.
(1)试求出0≤x≤20和x>20时,y与x之间的函数关系;
(2)小明家第二季度用水量的情况如下:
月份 | 四月 | 五月 | 六月 |
用水量(m3) | 15 | 17 | 21 |
小明家这个季度共缴纳水费多少元?
【答案】
(1)解:因为月用水量不超过20m3时,按2元/m3计费,所以当0≤x≤20时,y与x的函数表达式是y=2x;
因为月用水量超过20m3时,其中的20m3仍按2元/m3收费,超过部分按2.6元/m3计费,所以当x>20时,y与x的函数表达式是y=2×20+2.6(x﹣20),
即y=2.6x﹣12;
综上所述,y= ![]()
(2)解:因为小明家四、五月份的用水都不超过20m3,六月份的用水超过20m3,
所以把x=15代入2x中,得2×15=30(元);
把17代入2x中,得2×17=34(元);
把x=21代入2.6x﹣12中,得2.6×21﹣12=42.6(元).
∴小花家这个季度共缴纳水费:30+34+42.6=106.6(元).
答:小花家这个季度共缴纳水费1066元
【解析】因为月用水量不超过20m3时,按2元/m3计费,所以当0≤x≤20时,y与x的函数表达式是y=2x;因为月用水量超过20m3时,其中的20m3仍按2元/m3收费,超过部分按2.6元/m3计费,所以当x>20时,y与x的函数表达式是y=2×20+2.6(x﹣20);(2)因为小明家四、五月份的用水都不超过20m3,六月份的用水超过20m3,分别代入解析式,求出结果即可.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】请在横线上和括号内填上推导内容或依据.
如图,已知 ![]() ,
, ![]() ,求证:
,求证: ![]() .
.
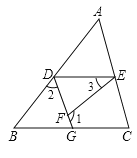
证明: ![]() (已知),
(已知),
![]() ( ),
( ),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
∵![]() (已知),
(已知),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
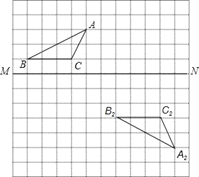
【题目】在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,若存在一个内角角度,是另外一个内角角度的
中,若存在一个内角角度,是另外一个内角角度的![]() 倍(
倍(![]() 为大于1的正整数),则称
为大于1的正整数),则称![]() 为
为![]() 倍角三角形.例如,在
倍角三角形.例如,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,所以
,所以![]() 为3倍角三角形.
为3倍角三角形.
(1)在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 为________倍角三角形;
为________倍角三角形;
(2)若![]() 是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的
是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的![]() ,求
,求![]() 的最小内角.
的最小内角.
(3)若![]() 是2倍角三角形,且
是2倍角三角形,且![]() ,请直接写出
,请直接写出![]() 的最小内角的取值范围.
的最小内角的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2020年83岁的钟南山奋战在抗击疫情的最前线,成为全国人民最敬佩的硬核男神,他有强健的身体,这都是得益于几十年如一日的坚持锻炼.在本次疫情中打败新冠肺炎还需要自身免疫力,同学们都应该加强身体锻炼,为了了解同学们在线上教学中体育锻炼的情况,在返校后某初中对600名初一学生进行了体育测试,其中对仰卧起坐成绩进行了整理,绘制成如下不完整的统计图:

根据统计图,回答下列问题.
(1)请将条形统计图补充完整;
(2)扇形统计图中,![]() =_____,得8分所对应扇形的圆心角度数为_____;
=_____,得8分所对应扇形的圆心角度数为_____;
(3)若本校共有3000名初一学生,请估算体育测试成绩为10分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
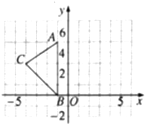
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=°.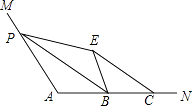
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理﹣﹣“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2 . 小明尝试对它进行证明,部分过程如下:
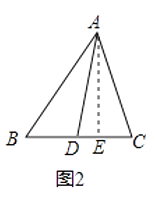
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2 ,
同理可得:AC2=AE2+CE2 , AD2=AE2+DE2 ,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=…
(1)请你完成小明剩余的证明过程;
理解运用: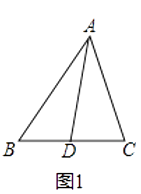
(2)①在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=;
②如图3,⊙O的半径为6,点A在圆内,且OA=2 ![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
拓展延伸: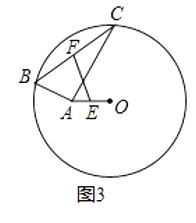
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5 ![]() ,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
请你利用上面的方法和结论,求出AD长的最大值.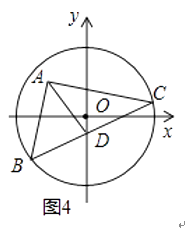
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com