
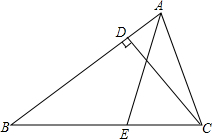
 如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数.
如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数. 分析 先根据CD为△ABC的高,求∠BDC的度数,再结合图形根据角的和差求出∠ACD的度数,利用三角形的内角和求∠BAC,因AE为△ABC的角平分线,所以可得∠CAE,最后利用△AFC的内角和为180°,求得∠AFC的度数.
解答 解:∵CD为△ABC的高,
∴∠BDC=90°,
∵∠B=30°,
∴∠BCD=60°,
又∵∠ACB=75°,
∴∠ACD=∠ACB-∠BCD=15°,
∴∠BAC=180°-∠B-∠ACB=75°,
∵AE为△ABC的角平分线,
∴∠CAE=$\frac{1}{2}$∠BAC=37.5°,
∴∠AFC=180°-∠CAE-∠ACD=127.5°.
点评 此题考查三角形的角平分线、高的意义,三角形的内角和定理,结合图形,理解题意,灵活运用定义域定理解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).
如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com