
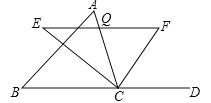
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
【答案】(1)5;(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
【解析】
试题分析:(1)根据平行线的性质以及角平分线的性质得出∠OEC=∠OCE,∠OFC=∠OCF,证出OE=OC=OF,∠ECF=90°,由勾股定理求出EF,即可得出答案;
(2)根据平行四边形的判定以及矩形的判定得出即可.
试题解析:(1)证明:∵EF交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠OCE=∠BCE,∠OCF=∠DCF,∵MN∥BC,∴∠OEC=∠BCE,∠OFC=∠DCF,∴∠OEC=∠OCE,∠OFC=∠OCF,∴OE=OC,OF=OC,∴OE=OF;
∵∠OCE+∠BCE+∠OCF+∠DCF=180°,∴∠ECF=90°,在Rt△CEF中,由勾股定理得:EF=![]() =10,∴OC=OE=
=10,∴OC=OE=![]() EF=5;
EF=5;
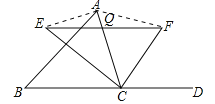
(2)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:
连接AE、AF,如图所示:
当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形,∵∠ECF=90°,∴平行四边形AECF是矩形.


科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
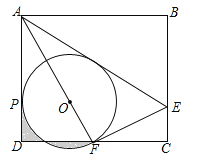
【题目】如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④
CE;④![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
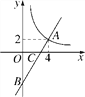
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
(1)求函数y=![]() 和y=kx+b的解析式;
和y=kx+b的解析式;
(2)已知直线AB与x轴相交于点C,在第一象限内,求反比例函数y=![]() 的图象上一点P,使得S△POC=9.
的图象上一点P,使得S△POC=9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝首个“中国农民丰收节”,海淀区将在海淀公园举办京西稻收割节活动,京西稻是著名农业作物,颗粒圆润,晶莹明亮,稻谷每粒重约0.000028千克.将0.000028用科学记数法表示为( )
A. 2.8×10﹣5B. 2.8×10﹣6C. 28×10﹣6D. 0.28×10﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知一次函数y=x﹣1的图象经过P1(x1 , y1)、P2(x2 , y2)两点,若x1<x2 , 则y1y2(填“>”,“<”或“=”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com