
【题目】如图,风车的支杆OE垂直于桌面,风车中心O到桌面的距离OE为25cm,小小风车在风吹动下绕着中心O不停地转动,转动过程中,叶片端点A、B、C、D在同一圆O上,已知⊙O的半径为10cm,
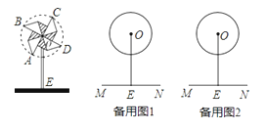
(1)风车在转动过程中,当∠AOE=30°时,求点A到桌面的距离.
(2)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm所经过的路线长.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)作A1F⊥MN于点F,A1G⊥OE于点G,在Rt△A1OG中,利用三角函数可求得OG,从而得出点A到桌面的距离A1F;
(2)作A2H⊥MN于H,则A2H=20cm,作A2D⊥OE于点D,则DE=A2H.在Rt△A2OD中,由特殊角的三角函数得∠A2OD=60°,由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°,从而得出点A所经过的路径长.
解:(1)如图(1),点A运动到点A1的位置时∠AOE=30°,作A1F⊥MN于点F,A1G⊥OE于点G,
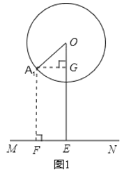
∴A1F=GE.
在Rt△A1OG中,
∵∠A1OG=30°,OA1=10cm,
∴OG=OA1cos30°=10×![]() cm.
cm.
∵OE=25 cm,
∴GE=OEOG=25![]() (cm),
(cm),
∴A1F=GE=25![]() (cm),
(cm),
答:点A到桌面的距离是25![]() 厘米;
厘米;
(2)如图(2),点A在旋转过程中运动到点A2、A3的位置时,点A到桌面的距离等于20厘米,作A2H⊥MN于H,则A2H=20 cm,作A2D⊥OE于点D,
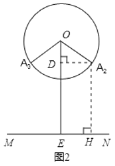
∴DE=A2H,
∵OE=25 cm,
∴OD=OEDE=2520=5 cm,
在Rt△A2OD中,OA2=10 cm,
∴cos∠A2OD=![]() ,
,
∴∠A2OD=60°.
由圆的对称性可知,∠A3OA2=2∠A2OD=120°,
∴点A相对于桌面的高度不超过20cm所经过的路线长为:![]() cm.
cm.
答:点A相对于桌面的高度不超过20cm所经过的路线长为![]() 厘米.
厘米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a>0)的对称轴为x=-1,交x轴的一个交点为(x1,0),且0<x1<1, 则下列结论:①b>0,c<0;②a-b+c>0 ;③b<a ④ 3a+c>0,⑤9a-3b+c>0,其中正确的命题有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的![]() 中,
中,![]() ,且
,且![]() 为
为![]() 上一点.今打算在
上一点.今打算在![]() 上找一点
上找一点![]() ,在
,在![]() 上找一点
上找一点![]() ,使得
,使得![]() 与
与![]() 全等,以下是甲、乙两人的作法:
全等,以下是甲、乙两人的作法:
(甲)连接![]() ,作
,作![]() 的中垂线分别交
的中垂线分别交![]() 、
、![]() 于
于![]() 点、
点、![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
(乙)过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,过
点,过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )

A. 两人皆正确B. 两人皆错误
C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AB=2cm,线段AB与直线l之间的距离为![]() cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
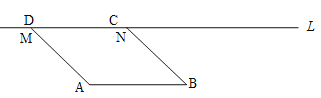
(1)当t=____s时,□ABCD为矩形;
(2)线段CD在直线l上移动过程中,当□ABCD为菱形时,求线段CD运动时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是直线___________,顶点坐标是___________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内画出该抛物线的图像;


(3)根据图像回答,![]() 有实数根,此时
有实数根,此时![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为
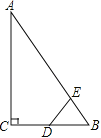
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() ,比如指数式
,比如指数式![]() 可以转化为对数式
可以转化为对数式![]() ,对数式
,对数式![]() ,可以转化为指数式
,可以转化为指数式![]() .
.
我们根据对数的定义可得到对数的一个性质:
![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),理由如下:
),理由如下:
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,由对数的定义得
,由对数的定义得![]()
又∵![]()
∴![]()
根据阅读材料,解决以下问题:
(1)将指数式![]() 转化为对数式________;
转化为对数式________;
(2)求证:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )
)
(3)拓展运用:计算![]() ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com