
【题目】已知等腰三角形ABC的三个顶点都在直径为10的⊙O上,如果圆心O到BC的距离为3,那么三角形ABC的面积为_________.
【答案】8或32或30.72(![]() )
)
【解析】
此题分情况考虑:①当BC是底边,△ABC是锐角三角形时;②当BC是底边,△ABC是钝角三角形时;③当BC是腰时;分别根据勾股定理和垂径定理求出等腰三角形的底边长和底边上的高,根据三角形的面积公式即可得到结论.
解:分情况讨论:
①当BC是底边,△ABC是锐角三角形时,连接AO并延长到BC于点D,如图1,
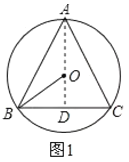
∵AB=AC,O为外心,
∴AD⊥BC,
在Rt△BOD中,OB=5,OD=3,
∴BD=![]() ,
,
∴AD=5+3=8,BC=2BD=8,
∴三角形ABC的面积=![]() ×8×8=32;
×8×8=32;
②当BC是底边,△ABC是钝角三角形时,连接AO交BC于点D,如图2所示,
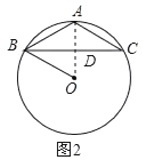
在Rt△BOD中,OB=5,OD=3,
∴BD=![]() ,
,
∴AD=53=2,BC=2BD=8,
∴三角形ABC的面积=![]() ×2×8=8,
×2×8=8,
③当BC是腰时,连接BO并延长到AC于点E,作OD⊥BC于点D,如图3所示,
在Rt△BOD中,OB=5,OD=3,
∴BD=![]() ,
,
∴BC=2BD=8,
设OE=x,
在Rt△COE中,![]() ,
,
在Rt△BCE中,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∴三角形ABC的面积=![]() ,
,

故答案为:8或32或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。

(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()

(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
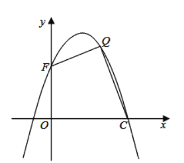
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
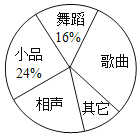
【题目】某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
(1)在此次调查中,该校一共调查了 名学生;
(2)a= ;b= ;
(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;
(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平方运算和开方运算是互逆运算,如:![]() ,那么
,那么![]() ,那么如何将双重二次根式
,那么如何将双重二次根式![]()
![]() 化简呢?如能找到两个数
化简呢?如能找到两个数![]()
![]() ,使得
,使得![]() 即
即![]() ,且使
,且使![]() 即
即![]() ,
,
那么![]()
![]() ,双重二次根式得以化简;
,双重二次根式得以化简;
例如化简:![]() ;
; ![]() 且
且![]() ,
,![]()
![]()
由此对于任意一个二次根式只要可以将其化成![]() 的形式,且能找到
的形式,且能找到![]() 使得
使得![]() ,且
,且![]() ,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
(1)填空:![]() _________________;
_________________; ![]() __________________;
__________________;
(2)化简:① ![]() ②
②![]()
(3)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,风车的支杆OE垂直于桌面,风车中心O到桌面的距离OE为25cm,小小风车在风吹动下绕着中心O不停地转动,转动过程中,叶片端点A、B、C、D在同一圆O上,已知⊙O的半径为10cm,
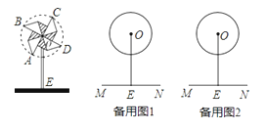
(1)风车在转动过程中,当∠AOE=30°时,求点A到桌面的距离.
(2)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm所经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
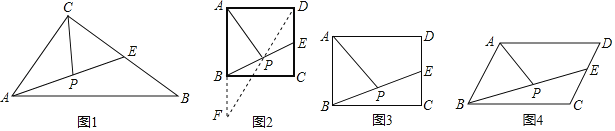
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某座抛物线型的隧道示意图,已知路面AB宽24米,抛物线最高点C到路面AB的距离为8米,为保护来往车辆的安全,在该抛物线上距路面AB高为6米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.
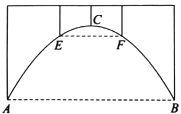
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com