
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

【答案】(1)15°;(2)BE=![]() .(3)AC=20.
.(3)AC=20.
【解析】
(1)根据“准互余三角形”的定义构建方程即可解决问题;
(2)只要证明△CAE∽△CBA,可得CA2=CECB,由此即可解决问题;
(3)如图②中,将△BCD沿BC翻折得到△BCF.只要证明△FCB∽△FAC,可得CF2=FBFA,设FB=x,则有:x(x+7)=122,推出x=9或﹣16(舍弃),再利用勾股定理求出AC即可;
(1)∵△ABC是“准互余三角形”,∠C>90°,∠A=60°,
∴2∠B+∠A=60°,
解得,∠B=15°;
(2)如图①中,

在Rt△ABC中,∵∠B+∠BAC=90°,∠BAC=2∠BAD,
∴∠B+2∠BAD=90°,
∴△ABD是“准互余三角形”,
∵△ABE也是“准互余三角形”,
∴只有2∠B+∠BAE=90°,
∵∠B+∠BAE+∠EAC=90°,
∴∠CAE=∠B,∵∠C=∠C=90°,
∴△CAE∽△CBA,可得CA2=CECB,
∴CE=![]() ,
,
∴BE=5﹣![]() =
=![]() .
.
(3)如图②中,将△BCD沿BC翻折得到△BCF.
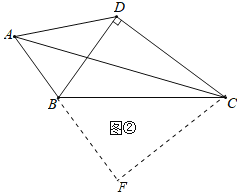
∴CF=CD=12,∠BCF=∠BCD,∠CBF=∠CBD,
∵∠ABD=2∠BCD,∠BCD+∠CBD=90°,
∴∠ABD+∠DBC+∠CBF=180°,
∴A、B、F共线,
∴∠A+∠ACF=90°
∴2∠ACB+∠CAB≠90°,
∴只有2∠BAC+∠ACB=90°,
∴∠FCB=∠FAC,∵∠F=∠F,
∴△FCB∽△FAC,
∴CF2=FBFA,设FB=x,
则有:x(x+7)=122,
∴x=9或﹣16(舍去),
∴AF=7+9=16,
在Rt△ACF中,AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,抛物线y=ax2﹣4ax+c与直线y=kx+1(k≠0)交于y轴上一点A和第一象限内一点B,该抛物线顶点H的纵坐标为5.
(1)求抛物线的解析式;
(2)连接AH、BH,抛物线的对称轴与直线y=kx+1(k≠0)交于点K,若S△AHB=![]() ,求k的值;
,求k的值;
(3)在(2)的条件下,点P是直线AB上方的抛物线上的一动点(如图2),连接PA.当∠PAB=45°时,
ⅰ)求点P的坐标;
ⅱ)已知点M在抛物线上,点N在x轴上,当四边形PBMN为平行四边形时,请求出点M的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=6,BC=8.
(1)求对角线AC的长;
(2)点E是线段CD上的一点,把△ADE沿着直线AE折叠.点D恰好落在线段AC上,与点F重合,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 是反比例函数.
是反比例函数.
(1)求m的值;
(2)指出该函数图象所在的象限,在每个象限内,y随x的增大如何变化?
(3)判断点(![]() ,2)是否在这个函数的图象上.
,2)是否在这个函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知射线AP是△ABC的外角平分线,连结PB、PC.
(1)如图1,若BP平分∠ABC,且∠ACB=30°,写出∠APB的度数.
(2)如图1,若P与A不重合,求证:AB+AC<PB+PC.
(3)如图2,若过点P作PM⊥BA,交BA延长线于M点,且∠BPC=∠BAC,求:![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,A为x轴负半轴上的点,B为y轴负半轴上的点.

(1)如图①,以A点为顶点,AB为腰在第三象限作等腰Rt△ABC.若已知A(﹣2,0)B(0,﹣4),试求C点的坐标;
(2)如图②,若点A的坐标为(﹣2![]() ,0),点B的坐标为(0,a),点D的纵坐标为b,以B为顶点,BA为腰作等腰Rt△ABD,当B点沿y轴负半轴向下运动且其他条件都不变时,求b﹣a的值;
,0),点B的坐标为(0,a),点D的纵坐标为b,以B为顶点,BA为腰作等腰Rt△ABD,当B点沿y轴负半轴向下运动且其他条件都不变时,求b﹣a的值;
(3)如图③,E为x轴负半轴上的一点,且OB=OE,OF⊥EB于点F,以OB为边在第四象限作等边△OBM,连接EM交OF于点N,探究EM-ON与EN的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com