
����Ŀ����ֱ������ϵ�У�AΪx�Ḻ�����ϵĵ㣬BΪy�Ḻ�����ϵĵ㣮

��1����ͼ�٣���A��Ϊ���㣬ABΪ���ڵ�������������Rt��ABC������֪A����2��0��B��0����4��������C������ꣻ
��2����ͼ�ڣ�����A������Ϊ����2![]() ��0������B������Ϊ��0��a������D��������Ϊb����BΪ���㣬BAΪ��������Rt��ABD����B����y�Ḻ���������˶�����������������ʱ����b��a��ֵ��
��0������B������Ϊ��0��a������D��������Ϊb����BΪ���㣬BAΪ��������Rt��ABD����B����y�Ḻ���������˶�����������������ʱ����b��a��ֵ��
��3����ͼ�ۣ�EΪx�Ḻ�����ϵ�һ�㣬��OB��OE��OF��EB�ڵ�F����OBΪ���ڵ����������ȱ���OBM������EM��OF�ڵ�N��̽��EM-ON��EN��������ϵ��
���𰸡���1��C����6����2������2��2![]() ����3��EN��
����3��EN��![]() ��EM��ON�������ɼ�����
��EM��ON�������ɼ�����
��������
��1����CQ��OA�ڵ�Q������֤����AQC�ա�BOA����QC=AO��AQ=BO�����������Ϳ������C�����ꣻ
��2����DP��OB�ڵ�P������֤����AOB�ա�BPD������AO=BP=OB-PO=-a-��-b��=b-aΪ��ֵ��
��3����BH��EB��B�����������Եó���1=30������2=��3=��EMO=15������EOF=��BMG=45����EO=BM������֤����ENO�ա�BGM����GM=ON������EM-ON=EM-GM=EG�������ƽ���߷��߶γɱ��������Ϳ��Եó�EN=EM-ON��һ�룮
��1����ͼ��1����CQ��OA�ڵ�Q��

���AQC��90��
�ߡ�ABC�ǵ���Rt����
��AC��AB����CAB��90����
���ACQ����BAO��
����AQC����BOA��
 ��
��
���AQC�ա�BOA��
��CQ��AO��AQ��BO��
��A����2��0����B��0����4����
��OA��2��OB��4��
��CQ��2��AQ��4��
��OQ��6��
��C����6����2����
��2����ͼ��2����DP��OB�ڵ�P��

���BPD��90����
�ߡ�ABD�ǵ���Rt����
��AB��BD����ABD����ABO+��OBD��90����
���ABO����BDP��
����AOB����BPD��
 ��
��
���AOB�ա�BPD��
��AO��BP��
��BP��OB��PO����a������b����b��a��
��A����2![]() ��0����
��0����
��OA��2![]() ��
��
��b��a��2![]() ��
��
�൱B����y�Ḻ���������˶�ʱAO��BP��b��a��2![]() ��
��
��3����ͼ��3����ME�Ͻ�ȡMG��ON������BG��

�ߡ�OBM�ǵȱ������Σ�
��BO��BM��MO����OBM����OMB����BOM��60����
��EO��MO����EBM��105������1��30����
��OE��OB�� ��OE��OM��BM��
���3����EMO��15����
���BEM��30������BME��45����
��OF��EB��
���EOF��45��
���EOF����BME��
����ENO����BGM��
 ��
��
���ENO�ա�BGM��
��BG��EN��
��ON��MG��
���2����3��
���2��15����
���EBG��90��
��BG��![]() EG��
EG��
��EN��![]() EG��
EG��
��EG��EM��GM��
��EN��![]() ��EM��GM����
��EM��GM����
��EN��![]() ��EM��ON��.
��EM��ON��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0����ͼ���뷴��������y=![]() ��k��0����ͼ���ڵ�һ���������ڵ�����A��B����y�ύ��C�㣮����A��AD��y�ᣬ����Ϊ��D��AD=8��OC=2��tan��ACD=2����B������Ϊ��m����4����
��k��0����ͼ���ڵ�һ���������ڵ�����A��B����y�ύ��C�㣮����A��AD��y�ᣬ����Ϊ��D��AD=8��OC=2��tan��ACD=2����B������Ϊ��m����4����
��1����÷�����������һ�κ����Ľ���ʽ��
��2��ֱ��д����xȡ��ֵʱ��ax+b��![]() ��0������
��0������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ε������ڽ�����������2��+��=90������ô���dz�������������Ϊ����������������
��1������ABC��������������������C��90�㣬��A=60�������B=�� ���㣻
��2����ͼ�٣���Rt��ABC�У���ACB=90�㣬AC=4��BC=5����AD�ǡ�BAC��ƽ���ߣ�����֤����ABD�����������������������ڱ�BC���Ƿ���ڵ�E�����ڵ�D����ʹ����ABEҲ�����������������������ڣ������BE�ij����������ڣ���˵�����ɣ�
��3����ͼ�ڣ����ı���ABCD�У�AB=7��CD=12��BD��CD����ABD=2��BCD������ABC��������������������Խ���AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
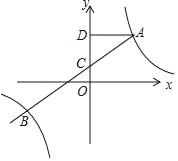
����Ŀ����ͼ��ֱ��y��2x+4��x�ᡢy��ֱ��ڵ�A��B����OBΪ�ױ���y���Ҳ���������OBC������OBC��y���۵���ʹ��Cǡ������ֱ��AB�ϣ����C������Ϊ��������

A.��1��2��B.��4��2��C.��3��2��D.����1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x���������ཻ��A��B���㣬��y���ཻ�ڵ�C���Գ���Ϊֱ��x=2����OA=OC�������н��ۣ���abc��0����9a+3b+c��0����c����1��������x�ķ���ax2+bx+c=0��a��0����һ����Ϊ��![]() ������������������P��x1��y1����Q��x2��y2������x1��2��x2����x1+x2��4����y1��y2��������ȷ�Ľ����У�������
������������������P��x1��y1����Q��x2��y2������x1��2��x2����x1+x2��4����y1��y2��������ȷ�Ľ����У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+4��x���ཻ�ڵ�A����y���ཻ�ڵ�B��
x+4��x���ཻ�ڵ�A����y���ཻ�ڵ�B��

��1������AOB�������
��2����B����ֱ��BC��x���ཻ�ڵ�C������ABC�������16�����C�����ꣻ
��3����P����������һ�㣬��PA=PB����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ���Rt��ABC������BAC=90������E��AC�ϣ��Ҳ����A��C�غ���������ABC���ⲿ������Rt��CED��ʹ��CED=90��������AD���ֱ���AB��ADΪ�ڱ���ƽ���ı���ABFD������AF��
��1����֤����AEF�ǵ���ֱ����������
��2����ͼ2������CED�Ƶ�C��ʱ����ת������E���߶�BC��ʱ������AE����֤��AF=![]() AE��
AE��
��3����ͼ3������CED�Ƶ�C������ʱ����ת����ƽ���ı���ABFDΪ����������CED����ABC���·�ʱ����AB=2![]() ��CE=2�����߶�AE�ij���
��CE=2�����߶�AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �У�
��![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.

��1��ֱ��д��![]() ��
��![]() ��������ϵ��
��������ϵ��
��2����![]() �����ã�1���Ĺ�ϵ�����
�����ã�1���Ĺ�ϵ�����![]() �Ķ�����
�Ķ�����
��3�����ã�2���Ľ�������ж�![]() ��
��![]() ��
��![]() ��������ϵ����֤��.
��������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��O�ǵȱ�![]() ��һ��
��һ��![]() ��
��![]() �Ƶ�C��˳ʱ�뷽����ת
�Ƶ�C��˳ʱ�뷽����ת![]() ��
��![]() ,����
,����![]() ��֪
��֪![]()
![]() ��
��
![]() ��֤��
��֤��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
![]() ��
��![]() ʱ,���ж�
ʱ,���ж�![]() ����״,��˵�����ɣ�
����״,��˵�����ɣ�
![]() ̽������
̽������![]() Ϊ���ٶ�ʱ,
Ϊ���ٶ�ʱ,![]() �ǵ��������Σ�
�ǵ��������Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com