
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.

(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标;
(3)若P是坐标轴上一点,且PA=PB,求P的坐标.
【答案】(1)12;(2)(﹣14,0)或(2,0);(3)P(-![]() ,0)或(0,-2.5)
,0)或(0,-2.5)
【解析】
(1)分别把x=0和y=0代入y=![]() x+4,解之,得到点B和点A的坐标,根据三角形的面积公式,计算求值即可,
x+4,解之,得到点B和点A的坐标,根据三角形的面积公式,计算求值即可,
(2)根据“过B点作直线BC与x轴相交于点C,若△ABC的面积是16”,结合点B的坐标,分两种情况求出线段AC的长,即可得到答案;
(3)分P在x轴上和P在y轴上两种情况,利用勾股定理求解即可.
(1)把x=0代入y=![]() x+4得:y=4,即点B的坐标为:(0,4),
x+4得:y=4,即点B的坐标为:(0,4),
把y=0代入y=![]() x+4得:
x+4得:![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
即点A的坐标为:(﹣6,0), S△AOB=![]() =12, 即△AOB的面积为12,
=12, 即△AOB的面积为12,
(2)根据题意得:点B到AC的距离为4,S△ABC=![]() =16,解得:AC=8,
=16,解得:AC=8,
即点C到点A的距离为8, ﹣6﹣8=﹣14,﹣6+8=2,
即点C的坐标为:(﹣14,0)或(2,0).
(3)当P在x轴上时,设P(x,0),由PA=PB得:(x+6)2=x2+42 ,解得x=-![]() ;
;
当P在y轴上时,设P(0,y),由PA=PB得:(y-4)2=y2+62 ,解得y=-2.5;
综上:P(-![]() ,0)或(0,-2.5)
,0)或(0,-2.5)


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
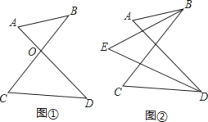
【题目】“8字”的性质及应用:
(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=![]() (∠A+∠C).
(∠A+∠C).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,A为x轴负半轴上的点,B为y轴负半轴上的点.

(1)如图①,以A点为顶点,AB为腰在第三象限作等腰Rt△ABC.若已知A(﹣2,0)B(0,﹣4),试求C点的坐标;
(2)如图②,若点A的坐标为(﹣2![]() ,0),点B的坐标为(0,a),点D的纵坐标为b,以B为顶点,BA为腰作等腰Rt△ABD,当B点沿y轴负半轴向下运动且其他条件都不变时,求b﹣a的值;
,0),点B的坐标为(0,a),点D的纵坐标为b,以B为顶点,BA为腰作等腰Rt△ABD,当B点沿y轴负半轴向下运动且其他条件都不变时,求b﹣a的值;
(3)如图③,E为x轴负半轴上的一点,且OB=OE,OF⊥EB于点F,以OB为边在第四象限作等边△OBM,连接EM交OF于点N,探究EM-ON与EN的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交ABCD的四条边于E、G、F、H四点,连接EG、GF、FH、HE.

(1)如图①,四边形EGFH的形状是___;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是___;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是___;
(4)如图④,在(3)的条件下,若AC⊥BD,四边形EGFH的形状是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形OABCDE中,点E(﹣2,0),将该正六边形向右平移a(a>0)个单位后,恰有两个顶点落在反比例函数y=![]() (k>0)的图象上,则k的值为__.
(k>0)的图象上,则k的值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,CE是中线,点F是CE的中点,DF⊥CE,点F为垂足.
(1)若AD=6,BD=8,求DE;
(2)若∠AEC=66°,求∠BCE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com