Question

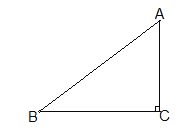
【题目】如图，△ABC中，AD是高，CE是中线，点F是CE的中点，DF⊥CE，点F为垂足．

（1）若AD=6，BD=8，求DE；

（2）若∠AEC=66°，求∠BCE的度数．

Answer 1

【答案】（1）5； （2）22°

【解析】试题分析：

(1)由勾股定理求得AB的长，再根据直角三角形斜边上的中线等于斜边的一半可得DE的长；

(2)根据题意可得△DCE，△EBD是等腰三角形，再结合三角形的一个外角等于和实验室不相邻的两个内角的和求解.

试题解析：

(1)因为AD是高，所以∠ADB=90°.

在Rt△ADB中，由勾股定理得：AB==10.

所以DE=10.

(2)因为DF⊥CF，F是CF的中点，所以DC=DE，所以∠DCE=∠DEC.

因为E是AB的中点，所以ED=EB，所以∠EDB=∠EBD.

设∠DCE=∠DEC=x，则∠EDB=∠EBD=2x.

因为∠AEC=∠ECB+∠EBC，所以66°=x+2x，则x=22°.

所以∠BCE的度数是22°.