
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
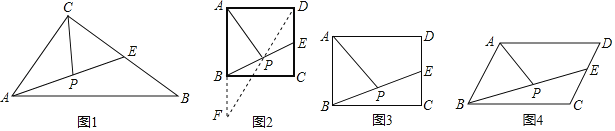
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
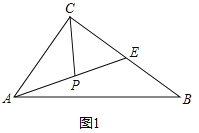
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)3
;(3)3![]() ;(4)△ABP的周长为4+
;(4)△ABP的周长为4+![]() .
.
【解析】
(1)利用勾股定理求出AE,再利用直角三角形斜边中线的性质即可解决问题.
(2)利用勾股定理求出DF,再利用直角三角形斜边中线的性质即可解决问题.
(3)如图3中,连接DP,延长DP交AB的延长线于H.利用全等三角形的性质以及勾股定理求出DH即可解决问题.
(4)如图4中,连接DP,延长DP交AB的延长线于H,作DK⊥BA交BA的延长线于K,AN⊥DH于N,EM⊥BC交BC的延长线于M.分别求出BP,AP即可解决问题.
解:(1)如图1中,
在Rt△ABC中,∵∠ACB=90°,AB=5,AC=3,
∴BC=![]()
∵E是BC的中点,
∴EC=EB=2,
∴AE=![]()
∵P是AE的中点,
∴PC=![]() AE=
AE=![]() .
.
故答案为![]() .
.
(2)如图2中,连接DP,延长DP交AB的延长线于F.

∵四边形ABCD是正方形,
∴AB=CD=4,AB∥CD,∠FAD=90°,
∴∠F=∠PDE,
∵PB=PE,∠FPB=∠EPD,
∴△FPB≌△DPE(AAS),
∴DP=PF,BF=DE=![]() CD=2,AF=AB+B4=2=6,
CD=2,AF=AB+B4=2=6,
在Rt△ADF中,DF=![]()
∵DP=PF,
∴AP=![]() DF=
DF=![]() ,
,
故答案为![]() .
.
(3)如图3中,连接DP,延长DP交AB的延长线于H.
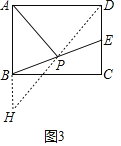
同法可证:∠DAB=90°,△HPB≌△DPE,
∴DE=BH=![]() CD=2,DP=PH,AHAB+BH=6,
CD=2,DP=PH,AHAB+BH=6,
在Rt△ADH中,DH=![]()
∵DP=PH,
∴PA=![]() DH=
DH=![]() .
.
(4)如图4中,连接DP,延长DP交AB的延长线于H,作DK⊥BA交BA的延长线于K,AN⊥DH于N,EM⊥BC交BC的延长线于M.
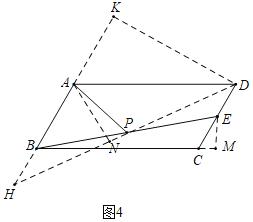
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,AB=CD=4,AD=BC=10,
在Rt△ADK中,∵∠KAD=60°,∠K=90°,AD=10,
∴AK=![]() AD=5,KD=
AD=5,KD=![]() AK=
AK=![]() ,
,
在Rt△ECM中,∵∠M=90°,∠ECM=60°,EC=![]() CD=2,
CD=2,
∴CM=![]() EC=1,EM=
EC=1,EM=![]() ,
,
在Rt△BEM中,BE=![]()
∵P是BE的中点,
∴PB=![]() EB=
EB=![]() ,
,
∵△PBH≌△PED,
∴DP=PH,DE=BH=2,HK=BH+AB+AK=2+4+5=11,
∴DH=![]()
∴PH=PD=7,
∵∠AHN=∠DHE,∠ANH=∠K=90°,
∴△HAN∽△HDK,
∴![]()
∴![]()
∴AN=![]() ,HN=
,HN=![]() ,
,
∴PN=PH﹣HN=7﹣![]() =
=![]() ,
,
∵AN⊥DH,
∴PA=![]()
∴△ABP的周长=AB+PA+PB=![]()


科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)求日销售利润W与X之间的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
(1)当k=3时,求函数图像与x轴的交点坐标;
(2)函数图像的对称轴与原点的距离为3,求k的值
(3)设二次函数图像上的一点P(x,y)满足![]() 时,y≤2,求k的取值范围。
时,y≤2,求k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料题:
浙教版九上作业本①第18页有这样一个题目:已知,如图一,P是正方形ABDC内一点,连接PA、PB、PC,若PC=2,PA=4,∠APC=135°,求PB的长.
小明看到题目后,思考了许久,仍没有思路,就去问数学老师,老师给出的提示是:将△PAC绕点A顺时针旋转90°得到△P'AB,再利用勾股定理即可求解本题. 请根据数学老师的提示帮小明求出图一中线段PB的长为 .
(方法迁移):已知:如图二,△ABC为正三角形,P为△ABC内部一点,若PC=1,PA=2,PB=![]() ,求∠APB的大小.
,求∠APB的大小.
(能力拓展):已知:如图三,等腰三角形ABC中∠ACB=120°,D、E是底边AB上两点且∠DCE=60°,若AD=2,BE=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是直线___________,顶点坐标是___________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内画出该抛物线的图像;


(3)根据图像回答,![]() 有实数根,此时
有实数根,此时![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
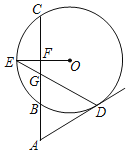
(1)求证明:AD是⊙D的切线;
(2)若∠A=60°,⊙O的半径为4,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )
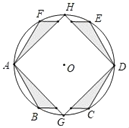
A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com