
【题目】阅读材料题:
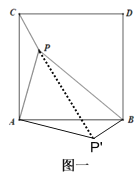
浙教版九上作业本①第18页有这样一个题目:已知,如图一,P是正方形ABDC内一点,连接PA、PB、PC,若PC=2,PA=4,∠APC=135°,求PB的长.
小明看到题目后,思考了许久,仍没有思路,就去问数学老师,老师给出的提示是:将△PAC绕点A顺时针旋转90°得到△P'AB,再利用勾股定理即可求解本题. 请根据数学老师的提示帮小明求出图一中线段PB的长为 .
(方法迁移):已知:如图二,△ABC为正三角形,P为△ABC内部一点,若PC=1,PA=2,PB=![]() ,求∠APB的大小.
,求∠APB的大小.
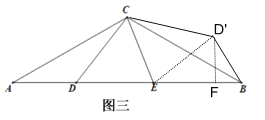
(能力拓展):已知:如图三,等腰三角形ABC中∠ACB=120°,D、E是底边AB上两点且∠DCE=60°,若AD=2,BE=3,求DE的长.
【答案】(1)6;(2)90°;(3)![]()
【解析】
如图一,根据旋转的性质可得△PAP'是等腰直角三角形,求出PP',然后求出∠PP'B=90°,利用勾股定理求出PB即可;
[方法迁移]:将△PAC绕点A顺时针旋转60°得到△P'AB,连接PP',根据旋转的性质可得△PAP'是等边三角形,利用勾股定理逆定理可证∠PBP'=90°,且∠BPP'=30°,问题得解;
[能力拓展]:将△CAD绕点C逆时针旋转120°得到△CBD',连接ED',易证△CDE≌△CD'E,可得DE=D'E,然后根据旋转的性质求出∠EBD'=60°,AD=BD'=2,过点D'作D'F⊥AB于F,根据含30°直角三角形的性质求出BF和D'F,然后利用勾股定理可求D'E,问题得解.
解:如图一,将△PAC绕点A顺时针旋转90°得到△P'AB,连接PP',
∴PA= P'A=4,PC= P'B=2,∠PAP'=90°,∠AP'B= ∠APC =135°,
∴∠PP'A=45°,
∴PP'![]() ,∠PP'B=135°-45°=90°,
,∠PP'B=135°-45°=90°,
∴![]() ;
;
[方法迁移]:
如图二,将△PAC绕点A顺时针旋转60°得到△P'AB,连接PP',
∴PA= P'A=2,PC= P'B=1,∠PAP'=60°,
∴△PAP'是等边三角形,
∴PP'= PA= 2,
∵![]() ,即
,即![]() ,
,
∴∠PBP'=90°,∠BPP'=30°,
∴∠APB=60°+30°=90°;

[能力拓展]:
如图三,将△CAD绕点C逆时针旋转120°得到△CBD',连接ED',
∴CD=CD',AD=BD'=2,∠DCD'=120°,
∵∠DCE=60°,
∴∠DCE=∠ECD'=60°,
又∵CE=CE,
∴△CDE≌△CD'E(SAS),
∴DE=D'E,
又∵∠A=∠ABC=![]() ,
,
∴∠A=∠CBD'=30°,
∴∠EBD'=60°,
过点D'作D'F⊥AB于F,
∴BF=![]() ,D'F=
,D'F=![]() ,
,
∴EF=2,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在公园有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() 公分.敏敏观察到高度
公分.敏敏观察到高度![]() 公分矮圆柱的影子落在地面上,其影长为
公分矮圆柱的影子落在地面上,其影长为![]() 公分;而高圆柱的部分影子落在墙上,如图所示.
公分;而高圆柱的部分影子落在墙上,如图所示.

已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为![]() 公分,且此刻她的影子完全落在地面上,则影长为多少公分?
公分,且此刻她的影子完全落在地面上,则影长为多少公分?
(2)若同一时间量得高圆柱落在墙上的影长为![]() 公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平方运算和开方运算是互逆运算,如:![]() ,那么
,那么![]() ,那么如何将双重二次根式
,那么如何将双重二次根式![]()
![]() 化简呢?如能找到两个数
化简呢?如能找到两个数![]()
![]() ,使得
,使得![]() 即
即![]() ,且使
,且使![]() 即
即![]() ,
,
那么![]()
![]() ,双重二次根式得以化简;
,双重二次根式得以化简;
例如化简:![]() ;
; ![]() 且
且![]() ,
,![]()
![]()
由此对于任意一个二次根式只要可以将其化成![]() 的形式,且能找到
的形式,且能找到![]() 使得
使得![]() ,且
,且![]() ,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
(1)填空:![]() _________________;
_________________; ![]() __________________;
__________________;
(2)化简:① ![]() ②
②![]()
(3)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABO中A(-1,3)、B(-4,0).
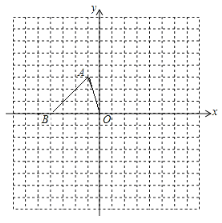
(1)画出△ABO绕着原点O按顺时针方向旋转90°后的图形,记为△![]() ;
;
(2)求△ABO外接圆圆心坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
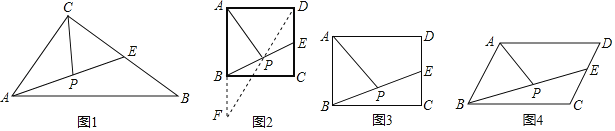
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,能更多让利于顾客并且商家平均每天能赢利1200元.
(2)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,
,![]() 之间的等量关系.
之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,易证
,易证![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断.
转化在一个三角形中即可判断.
![]() ,
,![]() ,
,![]() 之间的等量关系________;
之间的等量关系________;
(2)问题探究:如图②,在四边形![]() 中,
中,![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com