
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,能更多让利于顾客并且商家平均每天能赢利1200元.
(2)要想平均每天赢利2000元,可能吗?请说明理由.
【答案】(1)每件童装降价20元时,能更多让利于顾客并且商家平均每天能赢利1200元;(2)不可能,理由详见解析.
【解析】
(1)设每件童装降价x元,则销售量为(20+2x)件,根据总利润=每件利润 销售数量,即可得出关于x的一元二次方程,解之取其较大值即可得出结论
(2)设每件童装降价元,则销售量为(20+2y)件,根据总利润=每件利润 销售数量,即可得出关于y的一元二次方程,由根的判别式A<0可得出原方程无解,进而即可得出不可能每天盈利2000元.
(1)设每件童装降价![]() 元时,能更多让利于顾客并且商家平均每天能赢利1200元,得:
元时,能更多让利于顾客并且商家平均每天能赢利1200元,得:
![]()
![]()
![]()
∴![]() ,
,![]()
∵要更多让利于顾客
∴![]() 更符合题意
更符合题意
答:每件童装降价20元时,能更多让利于顾客并且商家平均每天能赢利1200元.
(2)不可能;
设每件桶童装降价![]() 元,则销售量为
元,则销售量为![]() 件,根据题意得:
件,根据题意得:
![]()
整理得:![]()
∵![]()
∴该方程无实数解
∴不可能每天盈利2000元.


科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
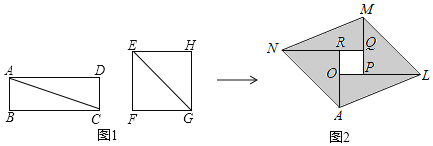
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
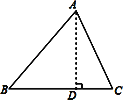
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:

(1)请你按照他们的解题思路过程完成解答过程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,则△DEF的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
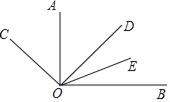
A. 113° B. 134° C. 136° D. 144°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,OA是⊙O的半径,点D为OA上的一动点,过D作线段CD⊥OA交⊙O于点F,过点C作⊙O的切线BC,B为切点,连接AB,交CD于点E.
(1)求证:CB=CE;
(2)如图2,当点D运动到OA的中点时,CD刚好平分![]() ,求证:△BCE是等边三角形;
,求证:△BCE是等边三角形;
(3)如图3,当点D运动到与点O重合时,若⊙O的半径为2,且∠DCB=45°,求线段EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解本校学生喜爱的球类运动,在本校范围内随机调查了部分学生,将收集的 数据绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:

(1)本次一共调查了多少名学生?
(2)补全条形统计图,并求出“足球”在扇形统计图中所占圆心角的度数;
(3)若已知该校有 500 名学生,请你根据调查的结果估计爱好“足球”和“排球”的学生共有多 少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com