
【题目】已知一次函数与反比例函数的图象交于点![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() )。
)。
(1)求这两个函数的函数关系式;
(2)当![]() 为何值时,一次函数值不小于反比例函数值.
为何值时,一次函数值不小于反比例函数值.
【答案】(1)反比例函数的关系式为y=![]() ,一次函数的关系式为y=x1;(2)x≤-3或0<x≤2.
,一次函数的关系式为y=x1;(2)x≤-3或0<x≤2.
【解析】
(1)用待定系数法求出一次函数及反比例函数的解析式;
(2)由函数的图像可观察出一次函数与反比例函数值的大小关系.
解:(1)设一次函数的关系式为y=kx+b,反比例函数的关系式为y=![]() ,
,
∵反比例函数的图像经过点Q(2,3),
∴3=![]() ,n=6.
,n=6.
∴反比例函数的关系式为y=![]() ;
;
将点P(3,m)的坐标代入上式得m=![]() =2,
=2,
∴点P的坐标为(-3,2);
由于一次函数y=kx+b的图像过P(3,2)和Q(2,3),
将P(-3,2)和Q(2,3)代入解析式得,
![]()
解得![]()
∴所求一次函数的关系式为y=x1.
(2)由 ,解得x=3或x=2,
,解得x=3或x=2,
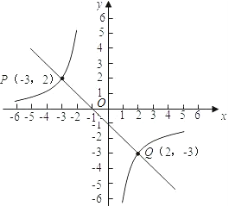
根据解析式画出两个函数图像如下图所示,
若使一次函数值不小于反比例函数值,则通过图像观察出:
x≤3或0<x≤2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
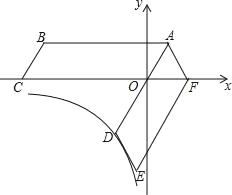
【题目】如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将平行四边形 ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上.若点D在反比例函数y=![]() (x<0)的图象上,则k的值为( )
(x<0)的图象上,则k的值为( )
A.4![]() B.12C.8
B.12C.8![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料题:
浙教版九上作业本①第18页有这样一个题目:已知,如图一,P是正方形ABDC内一点,连接PA、PB、PC,若PC=2,PA=4,∠APC=135°,求PB的长.
小明看到题目后,思考了许久,仍没有思路,就去问数学老师,老师给出的提示是:将△PAC绕点A顺时针旋转90°得到△P'AB,再利用勾股定理即可求解本题. 请根据数学老师的提示帮小明求出图一中线段PB的长为 .
(方法迁移):已知:如图二,△ABC为正三角形,P为△ABC内部一点,若PC=1,PA=2,PB=![]() ,求∠APB的大小.
,求∠APB的大小.
(能力拓展):已知:如图三,等腰三角形ABC中∠ACB=120°,D、E是底边AB上两点且∠DCE=60°,若AD=2,BE=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
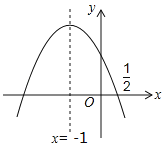
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
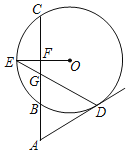
(1)求证明:AD是⊙D的切线;
(2)若∠A=60°,⊙O的半径为4,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
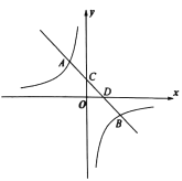
【题目】如图,一次函数![]() 的图象与双曲线
的图象与双曲线![]() 相交于A(-1,2)和B(2,b)两点,与y轴交于点C,与x轴交于点D.
相交于A(-1,2)和B(2,b)两点,与y轴交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)根据图象直接写出不等式![]() 的解集;
的解集;
(3)经研究发现:在y轴负半轴上存在若干个点P,使得![]() 为等腰三角形。请直接写出P点所有可能的坐标.
为等腰三角形。请直接写出P点所有可能的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
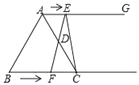
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s)
(1)填空:当t为 s时,△ABF是直角三角形;
(2)连接EF,当EF经过AC边的中点D时,四边形AFCE是否是特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
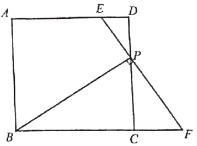
【题目】如图,正方形![]() 中,
中,![]() ,P为CD边上的一点,过P点作BP的垂线交AD于点E,交BC的延长线于点F.
,P为CD边上的一点,过P点作BP的垂线交AD于点E,交BC的延长线于点F.
(1)判断线段DE、CF、CP之间的数量关系,并说明理由.
(2)若![]() ,
,![]() ,写出y与x之间的函数关系式.
,写出y与x之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com