
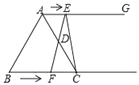
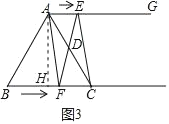
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s)
(1)填空:当t为 s时,△ABF是直角三角形;
(2)连接EF,当EF经过AC边的中点D时,四边形AFCE是否是特殊四边形?请证明你的结论.
【答案】(1)2或8;(2)四边形AFCE是平行四边形,证明见解析;
【解析】
(1)△ABF中,由△ABC是等边三角形可知∠B=60°≠90°,所以∠BAF与∠AFB可以等于90°,需分类讨论.画出图形,利用特殊三角函数值求出BF的长,除以点F速度即求得t的值.
(2)由AG∥BC可得∠EAD=∠FCD,∠AED=∠CFD,再加上点D为AC中点易证△ADE≌△CDF,进而得DE=DF,根据对角线互相平分的四边形为平行四边形可得四边形AFCE为平行四边形.再求此时AE、CF的长,说明∠AFC不等于90°和AF≠AE,排除四边形AFCE是菱形或矩形.
解:(1)∵等边△ABC中,BC=8cm
∴∠ABC=60°≠90°,AB=BC=8cm
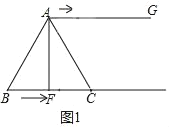
①如图1,若∠AFB=90°,则∠BAF=30°
∴BF=![]() AB=4cm
AB=4cm
∴t=BF÷2=2(s)
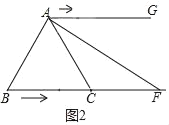
②如图2,若∠BAF=90°,则∠AFB=30°
∴BF=2AB=16cm
∴t=BF÷2=8(s)
故答案为:2或8.
(2)四边形AFCE是平行四边形,证明如下:
如图3,过点A作AH⊥BC于点H
∵∠ABC=60°,AB=8cm
∴sin∠ABC=![]() ,cos∠ABC=
,cos∠ABC=![]()
∴AH=![]() AB=4
AB=4![]() cm,BH=
cm,BH=![]() AB=4cm
AB=4cm
∵AG∥BC
∴∠EAD=∠FCD,∠AED=∠CFD
∵点D是AC中点
∴AD=CD
在△ADE与△CDF中
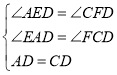
∴△ADE≌△CDF(AAS)
∴DE=DF
∴四边形AFCE是平行四边形
∴AE=CF
∵AE=t,CF=BC﹣BF=8﹣2t
∴t=8﹣2t
解得:t=![]()
∴AE=![]() cm,BF=
cm,BF=![]() cm
cm
∴BF>BH,AF>AH,∠AFC>90°
∴AF≠AE
∴四边形AFCE不是菱形或矩形,四边形AFCE是平行四边形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在公园有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() 公分.敏敏观察到高度
公分.敏敏观察到高度![]() 公分矮圆柱的影子落在地面上,其影长为
公分矮圆柱的影子落在地面上,其影长为![]() 公分;而高圆柱的部分影子落在墙上,如图所示.
公分;而高圆柱的部分影子落在墙上,如图所示.

已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为![]() 公分,且此刻她的影子完全落在地面上,则影长为多少公分?
公分,且此刻她的影子完全落在地面上,则影长为多少公分?
(2)若同一时间量得高圆柱落在墙上的影长为![]() 公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,能更多让利于顾客并且商家平均每天能赢利1200元.
(2)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
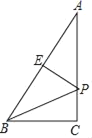
【题目】如图,在Rt△ABC中,∠A=30°,∠C=90°,E是斜边AB的中点,点P为AC边上一动点,若Rt△ABC的直角边AC=4,则PB+PE的最小值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
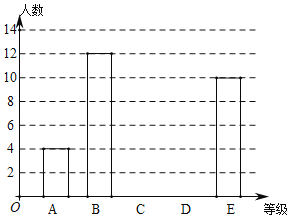
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
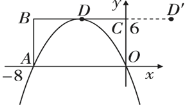
【题目】矩形OABC的顶点A(-8,0),C(0,6),点D是BC边上的中点,抛物线y=ax2+bx经过A,D两点,如图所示.
(1)求点D关于y轴的对称点D′的坐标及a,b的值;
(2)将抛物线y=ax2+bx向下平移,记平移后点A的对应点为A1,点D的对应点为D1,当抛物线平移到某个位置时,恰好使得点O是y轴上到A1,D1两点距离之和OA1+OD1最短的一点,求平移后的抛物线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,
,![]() 之间的等量关系.
之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,易证
,易证![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断.
转化在一个三角形中即可判断.
![]() ,
,![]() ,
,![]() 之间的等量关系________;
之间的等量关系________;
(2)问题探究:如图②,在四边形![]() 中,
中,![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com