
����Ŀ���ڹ���������ֱ��ˮƽ�����Ҹ߶Ȳ�һ��Բ��������Բ��������һ������滥�ഹֱ��ǽ����Բ����ǽ�ľ����Ϊ![]() ���֣������۲쵽�߶�
���֣������۲쵽�߶�![]() ���ְ�Բ����Ӱ�����ڵ����ϣ���Ӱ��Ϊ
���ְ�Բ����Ӱ�����ڵ����ϣ���Ӱ��Ϊ![]() ���֣�����Բ���IJ���Ӱ������ǽ�ϣ���ͼ��ʾ��
���֣�����Բ���IJ���Ӱ������ǽ�ϣ���ͼ��ʾ��

��֪���ڵ����ϵ�Ӱ�ӽ���ǽ�滥����ֱ������̫����Ϊƽ�й⣬�ڲ���Բ�������Ӱ�ӿ��ȵ�����£���ش��������⣺
��1��������������Ϊ![]() ���֣��Ҵ˿�����Ӱ����ȫ���ڵ����ϣ���Ӱ��Ϊ���ٹ��֣�
���֣��Ҵ˿�����Ӱ����ȫ���ڵ����ϣ���Ӱ��Ϊ���ٹ��֣�
��2����ͬһʱ�����ø�Բ������ǽ�ϵ�Ӱ��Ϊ![]() ���֣����Բ���ĸ߶�Ϊ���ٹ��֣�����ϸ���ͻ�����д����Ľ�����̣�������𰸣�
���֣����Բ���ĸ߶�Ϊ���ٹ��֣�����ϸ���ͻ�����д����Ľ�����̣�������𰸣�
���𰸡���1��������Ӱ��Ϊ![]() ���֣���2����Բ���ĸ߶�Ϊ
���֣���2����Բ���ĸ߶�Ϊ![]() ���֣�
���֣�
��������
��1������ͬһʱ�̣��ﳤ��Ӱ�ӳ����ȣ��������̼��ɽ�����⣮
��2����ͼ������![]() ����
����![]() ���ֱ����
���ֱ����![]() ��
��![]() �ij����ɽ�����⣮
�ij����ɽ�����⣮
�⣺��1����������Ӱ��Ϊ![]() ���֣�
���֣�
�����⣺![]() ��
��
���![]() �����֣���
�����֣���
�����飺![]() �Ƿ�ʽ���̵Ľ⣮
�Ƿ�ʽ���̵Ľ⣮
��������Ӱ��Ϊ![]() ���֣�
���֣�
��2����ͼ������![]() ����
����![]() ��
��
![]() ��
��
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
![]() ���֣�
���֣�
��![]() ���֣�������
���֣�������![]() ���ڵ����ϵ�Ӱ��Ϊ
���ڵ����ϵ�Ӱ��Ϊ![]() ���֣�
���֣�
![]() ��
��
![]() �����֣���
�����֣���
![]() �����֣���
�����֣���
�𣺸�Բ���ĸ߶�Ϊ![]() ���֣�
���֣�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ��������ij�ҿ�ݹ�˾��2017��3�·���5�·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ��
(1)��ÿ�ݹ�˾Ͷ�ݿ���ܼ�������ƽ����������
(2) ���ƽ��ÿ��ÿ������Ͷ�ݿ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ����2017��6�·ݵĿ��Ͷ������������ܣ�����������Ҫ���Ӽ���ҵ��Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCO��ƽ���ı��Σ�OA=2��AB=6����C��x��ĸ������ϣ���ƽ���ı��� ABCO�Ƶ�A��ʱ����ת�õ�ƽ���ı���ADEF��AD������O����Fǡ������x����������ϣ�����D�ڷ���������y=![]() ��x��0����ͼ���ϣ���k��ֵΪ��������
��x��0����ͼ���ϣ���k��ֵΪ��������
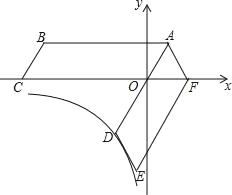
A.4![]() B.12C.8
B.12C.8![]() D.6
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��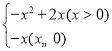 ��ͼ����ͼ��ʾ����ֱ��y��x+m���ͼ��ǡ��������ͬ�Ľ��㣬��m��ȡֵ��ΧΪ_____.
��ͼ����ͼ��ʾ����ֱ��y��x+m���ͼ��ǡ��������ͬ�Ľ��㣬��m��ȡֵ��ΧΪ_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y��ax2+bx+3��������ֱ��ڵ�A��B����3��0����C��1��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��1���������߽���ʽ��
��2������P�˶���ʲôλ��ʱ����PAB��������
��3������P��x��Ĵ��ߣ����߶�AB�ڵ�D���ٹ���P��PE��x�ύ�������ڵ�E������DE�������Ƿ���ڵ�Pʹ��PDEΪ����ֱ�������Σ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]()
��1����k=3ʱ������ͼ����x��Ľ������ꣻ
��2������ͼ��ĶԳ�����ԭ��ľ���Ϊ3����k��ֵ
��3������κ���ͼ���ϵ�һ��P��x��y������![]() ʱ��y��2����k��ȡֵ��Χ��
ʱ��y��2����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲���ֲ����Ϊ����߲˲������ƻ��Լס��������ͺ��߲˴�����и��죬����Ԥ�㣬����2�������ͺŴ����1�������ͺŴ�������ʽ�6��Ԫ������1�������ͺŴ����2�������ͺŴ��ﹲ���ʽ�48��Ԫ��
��1������1�������ͺź�1�������ͺŴ��������ʽ�ֱ��Ƕ�����Ԫ��
��2����֪����1�������ͺŴ����ʱ����5�죬����1�������ͺŴ�ŵ�ʱ����3�죬�û��ؼƻ�����ס��������߲˴��ﹲ8���������ʽ������Ͷ��128��Ԫ��Ҫ�����ʱ�䲻����35�죬�����м��ָ��췽�������ַ�������Ͷ���ʽ����٣������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
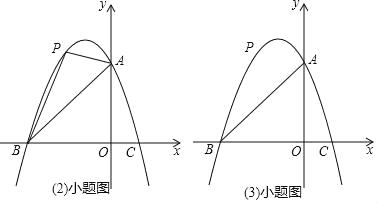
��̰������ҵ���ٵ�18ҳ������һ����Ŀ����֪����ͼһ��P��������ABDC��һ�㣬����PA��PB��PC����PC=2��PA=4����APC=135������PB�ij�.
С��������Ŀ��˼�������ã���û��˼·����ȥ����ѧ��ʦ����ʦ��������ʾ�ǣ�����PAC�Ƶ�A˳ʱ����ת90���õ���P'AB�������ù��ɶ���������Ȿ��. �������ѧ��ʦ����ʾ��С�����ͼһ���߶�PB�ij�Ϊ .
������Ǩ�ƣ�����֪����ͼ������ABCΪ�������Σ�PΪ��ABC�ڲ�һ�㣬��PC=1��PA=2��PB=![]() ,���APB�Ĵ�С.
,���APB�Ĵ�С.
��������չ������֪����ͼ��������������ABC�С�ACB=120����D��E�ǵױ�AB�������ҡ�DCE=60������AD=2��BE=3����DE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
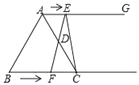
����Ŀ����ͼ��ʾ���ڵȱ�������ABC�У�BC��8cm������AG��BC����E�ӵ�A����������AG��lcm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt��s��
��1����գ���tΪ�� ��sʱ����ABF��ֱ�������Σ�
��2������EF����EF����AC�ߵ��е�Dʱ���ı���AFCE�Ƿ��������ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com