
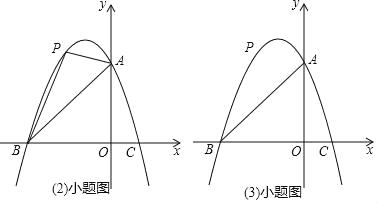
����Ŀ����֪����ͼ��������y��ax2+bx+3��������ֱ��ڵ�A��B����3��0����C��1��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��1���������߽���ʽ��
��2������P�˶���ʲôλ��ʱ����PAB��������
��3������P��x��Ĵ��ߣ����߶�AB�ڵ�D���ٹ���P��PE��x�ύ�������ڵ�E������DE�������Ƿ���ڵ�Pʹ��PDEΪ����ֱ�������Σ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��y����x2��2x+3 ��2������![]() ��
��![]() �� ��3�����ڣ�P����2��3����P��
�� ��3�����ڣ�P����2��3����P��![]() ��
��![]() ��
��
��������
��1���ô���ϵ������⣻��2������P��PH��x���ڵ�H����AB�ڵ�F��ֱ��AB����ʽΪy��x+3����P��t����t2��2t+3������3��t��0������F��t��t+3������PF����t2��2t+3����t+3������t2��3t������S��PAB��S��PAF+S��PBFд������ʽ�����������ֵ����3����P��t����t2��2t+3������3��t��0������D��t��t+3����PD����t2��3t����������y����x2��2x+3������x+1��2+4���ɶԳ���Ϊֱ��x����1��PE��x�ύ�������ڵ�E����yE��yP������E��P���ڶԳ���Գƣ�����![]() ����1����xE����2��xP����2��t����PE��|xE��xP|��|��2��2t|���ɡ�PDEΪ����ֱ�������Σ���DPE��90�㣬��PD��PE���ٷ�������ۣ��ٵ���3��t�ܩ�1ʱ��PE����2��2t���ڵ���1��t��0ʱ��PE��2+2t
����1����xE����2��xP����2��t����PE��|xE��xP|��|��2��2t|���ɡ�PDEΪ����ֱ�������Σ���DPE��90�㣬��PD��PE���ٷ�������ۣ��ٵ���3��t�ܩ�1ʱ��PE����2��2t���ڵ���1��t��0ʱ��PE��2+2t
�⣺��1����������y��ax2+bx+3����B����3��0����C��1��0��
��![]() ��ã�
��ã�![]()
�������߽���ʽΪy����x2��2x+3
��2������P��PH��x���ڵ�H����AB�ڵ�F
��x��0ʱ��y����x2��2x+3��3
��A��0��3��
��ֱ��AB����ʽΪy��x+3
�ߵ�P���߶�AB�Ϸ���������
����P��t����t2��2t+3������3��t��0��
��F��t��t+3��
��PF����t2��2t+3����t+3������t2��3t
��S��PAB��S��PAF+S��PBF��![]() PFOH+
PFOH+![]() PFBH��
PFBH��![]() PFOB��
PFOB��![]() ����t2��3t������
����t2��3t������![]() ��t+
��t+![]() ��2+
��2+![]()
���P�˶�������Ϊ����![]() ��
��![]() ������PAB������
������PAB������
��3�����ڵ�Pʹ��PDEΪ����ֱ��������
��P��t����t2��2t+3������3��t��0������D��t��t+3��
��PD����t2��2t+3����t+3������t2��3t
��������y����x2��2x+3������x+1��2+4
��Գ���Ϊֱ��x����1
��PE��x�ύ�������ڵ�E
��yE��yP������E��P���ڶԳ���Գ�
��![]() ����1
����1
��xE����2��xP����2��t
��PE��|xE��xP|��|��2��2t|
�ߡ�PDEΪ����ֱ�������Σ���DPE��90��
��PD��PE
�ٵ���3��t�ܩ�1ʱ��PE����2��2t
�ੁt2��3t����2��2t
��ã�t1��1����ȥ����t2����2
��P����2��3��
�ڵ���1��t��0ʱ��PE��2+2t
�ੁt2��3t��2+2t
��ã�t1��![]() ��t2��
��t2��![]() ����ȥ��
����ȥ��
��P��![]() ��
��![]() ��
��
������������P��������2��3����![]() ��
��![]() ��ʱʹ��PDEΪ����ֱ�������Σ�
��ʱʹ��PDEΪ����ֱ�������Σ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
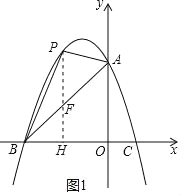
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ���е㣬
���е㣬![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ� ��
�ϣ� ��![]() ������
������![]() ����
����![]() ��
��![]() �ص�����������
�ص�����������![]() ���ܳ�Ϊ________
���ܳ�Ϊ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������Χ��ʮ�Ŵ�����Ľ���Ŀ�������ũҵ������ṹ�Ըĸ������ֲ�ṹ������������Ĵ�ṹ�������ֱ��ǣ�ˮ�������������ҵ����������ӹ����أ��︣�����ɽҩ����ź��ҵ��˫����IJ�ݮ��ҵ��Ŀǰ�������ֲ�ҵ����ʡ���⣮
ij��ؿ���Ľ�������飬��������ɽҩ�Ͳ�ݮ�������������г����飬������ɽҩ�Ͳ�ݮ��2�乲����170Ԫ������ɽҩ3��Ͳ�ݮ4�乲����300Ԫ��
��1����ɽҩ�Ͳ�ݮ�ĵ��ۣ�
��2�����ÿ��̹�����ɽҩ�Ͳ�ݮ��1000�䣬����ɽҩ���۵���Ϊ60Ԫ����ݮ�����۵���Ϊ70Ԫ���蹺��ɽҩx�䣬���������ΪyԪ��
����y����x�ĺ�����ϵʽ��
�����ڲ�ݮ�ı����ڽ϶̣��ÿ��̹�����ݮ����������ɽҩ������![]() ��Ҫʹ��������ɽҩ�Ͳ�ݮ��������������ÿ������һ�������������������������������ֵ��
��Ҫʹ��������ɽҩ�Ͳ�ݮ��������������ÿ������һ�������������������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
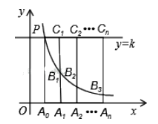
����Ŀ����ͼ��ֱ��y��k��˫����y��![]() �ཻ�ڵ�P������P��PA0��ֱ��x�ᣬ����ΪA0��x���ϵĵ�A0��A1��A2����An�ĺ���������������������A1��A2����An���ֱ���x��Ĵ��ߣ���˫����y��
�ཻ�ڵ�P������P��PA0��ֱ��x�ᣬ����ΪA0��x���ϵĵ�A0��A1��A2����An�ĺ���������������������A1��A2����An���ֱ���x��Ĵ��ߣ���˫����y��![]() ��k��0����ֱ��y��k�ֱ��ڵ�B1��B2����Bn�͵�C1��C2����Cn����
��k��0����ֱ��y��k�ֱ��ڵ�B1��B2����Bn�͵�C1��C2����Cn����![]() ��ֵΪ��������
��ֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC��90����AB��AC��AD��BC�ڵ�D��
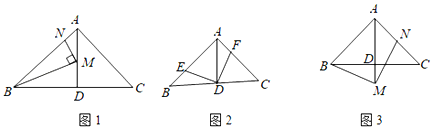
��1����ͼ1����M��N�ֱ���AD��AB�ϣ��ҡ�BMN��90��������AMN��30����AB��2ʱ�����߶�AM�ij���
��2����ͼ2����E��F�ֱ���AB��AC�ϣ��ҡ�EDF��90������֤��BE��AF��
��3����ͼ3����M��AD���ӳ����ϣ���N��AC�ϣ��ҡ�BMN��90������֤��AB+AN��![]() AM��
AM��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
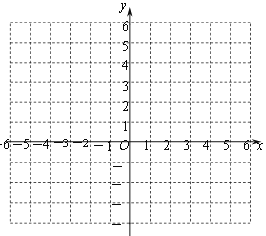
����Ŀ����֪���κ���y����x2��bx��c��b��cΪ��������ͼ���㣨2��3������3��0����
��1����b����c����
��2���ö��κ���ͼ����y��Ľ�������Ϊ����������Ϊ��
��3������������ϵ�л����ö��κ�����ͼ��
��4������ͼ����3��x��2ʱ��y��ȡֵ��Χ�ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ���ܳ���
���ܳ���![]() ����
����![]() ��
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���ٶ���
���ٶ���![]() ���������˶���ͬʱ��
���������˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���ٶ���
���ٶ���![]() ���������˶�����һ���㵽���
���������˶�����һ���㵽���![]() ʱ����һ����Ҳ��ֹ֮ͣ�˶��������˶�ʱ��Ϊ
ʱ����һ����Ҳ��ֹ֮ͣ�˶��������˶�ʱ��Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ���ͼ������ǣ� ��
֮��ĺ���ͼ������ǣ� ��
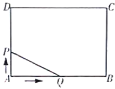
A.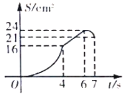 B.
B.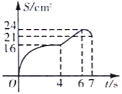
C.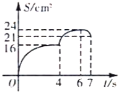 D.
D.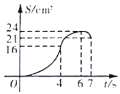
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У��Խ���
�У��Խ���![]() �Ĵ�ֱƽ���߽�ֱ��
�Ĵ�ֱƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() ��Ϊ______��
��Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪ��ABC�ı�![]() �ϵ�һ�㣬����O��OM��AB�ڵ�
�ϵ�һ�㣬����O��OM��AB�ڵ�![]() ������
������![]() �ľ�������߶�OM�ij������е����ͼ��
�ľ�������߶�OM�ij������е����ͼ��![]() ��ͼ��W������
��ͼ��W������![]() ����E��F����(���ڵ�F�����).
����E��F����(���ڵ�F�����).
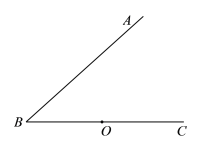
��1������![]() ��
��![]() �ڵ�
�ڵ�![]() �����BE=2��
�����BE=2��![]() ����MH�ij���
����MH�ij���
��2��������BC�Ƶ�B˳ʱ����ת�õ�����BD��ʹ�á�![]()
![]() ���ж�����BD��ͼ��
���ж�����BD��ͼ��![]() ������ĸ�������֤����
������ĸ�������֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com