
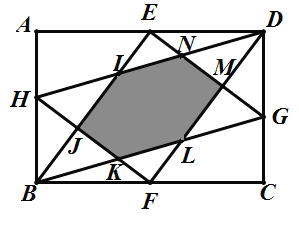
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别在
分别在![]() 、
、![]() 上, 且
上, 且![]() ,连结
,连结![]() ,则
,则![]() 与
与![]() 重叠部分六边形
重叠部分六边形![]() 的周长为________
的周长为________
【答案】9.8
【解析】
连结IK,LN,先证出四边形![]() 和四边形
和四边形![]() 是平行四边形,由已知和平行线的性质可得
是平行四边形,由已知和平行线的性质可得![]() 、
、![]() ,由等腰三角形的性质可得
,由等腰三角形的性质可得![]() 互相垂直且平分,进而证得四边形
互相垂直且平分,进而证得四边形![]() 和四边形
和四边形![]() 为菱形,利用相似三角形的性质和线段的计算求出六边形
为菱形,利用相似三角形的性质和线段的计算求出六边形![]() 的各个边长,即可得出周长.
的各个边长,即可得出周长.
解:如图,连结IK,LN,
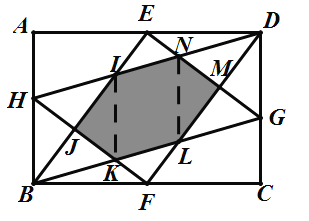
∵四边形![]() 是矩形,
是矩形,![]() ,
,
∴![]() ,
,
∵![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,
,![]() ,即
,即![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
由勾股定理得:![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() ,
,
∵ ,
,![]() ,即
,即![]() ,
,
又∵![]()
∴![]() ,
,
∴![]() ,
,
同理可得:![]() ,即
,即![]() ,
,
∴四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() ,
,![]() 得:
得:![]() 为等腰三角形,
为等腰三角形,
∴![]() 为HK中点,则
为HK中点,则![]() 垂直平分
垂直平分![]() ,
,
又由![]() ,
,![]() 得:
得:![]() 为等腰三角形,
为等腰三角形,
∴![]() 为BI中点,则
为BI中点,则![]() 垂直平分
垂直平分![]() ,
,
则![]() 互相垂直且平分,
互相垂直且平分,
∴四边形![]() 为菱形,
为菱形,![]() ,
,
同理得:四边形![]() 为菱形,
为菱形,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即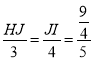 ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,
同理得:![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
由勾股定理得:![]() ,
,
∴![]() ,同理得:
,同理得:![]() ,
,
∴六边形![]() 的周长
的周长![]()
![]()
![]()
![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠ACB=∠EFD=90,△DEF,的顶点E与△ABC的斜边AB的中点重合.将△DEF绕点E旋转,旋转过程中,线段AC与线段EF相交于点Q,射线ED与射线BC相交于点P.
(1)求证:△AEQ∽△BPE;
(2)求证:PE平分∠BPQ;
(3)当AQ=2,AE=![]() ,求PQ的长.
,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.三角形的外心到三角形的三个顶点的距离相等
B.如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16
C.将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限
D.若关于x的一元一次不等式组![]() 无解,则m的取值范围是
无解,则m的取值范围是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
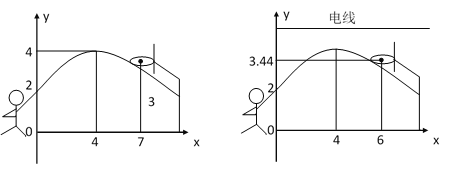
【题目】在小明的一次投篮中,球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米.篮球运行的轨迹为抛物线,篮球中心距离地面3米,通过计算说明此球能否投中.
探究一:若出手的角度、力度和高度都不变的情况下,求小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮筐中?
探究二:若出手的角度、力度和高度都发生改变的情况下,但是抛物线的顶点等其他条件不变,求小明出手的高度需要增加多少米才能将篮球投入篮筐中?
探究三:若出手的角度、力度都改变,出手高度不变,篮筐的坐标为(6,3.44),球场上方有一组高6米的电线,要想在篮球不触碰电线的情况下,将篮球投入篮筐中,直接写出二次函数解析式中a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相
交于点E,且AE平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠EAB=30°,OD=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
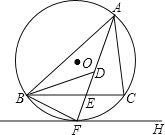
【题目】如图,![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,连结
,连结![]() .下列结论:①
.下列结论:①![]() 平分
平分![]() ;②连接
;②连接![]() ,点
,点![]() 为
为![]() 的外心;③
的外心;③![]() ;④若点
;④若点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是
的最小值是![]() .其中一定正确的是__________(把你认为正确结论的序号都填上).
.其中一定正确的是__________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
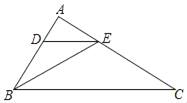
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,AE2=ADAB,∠ABE=∠ACB.
(1)求证:DE∥BC;
(2)如果S△ADE:S四边形DBCE=1:8,求S△ADE:S△BDE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
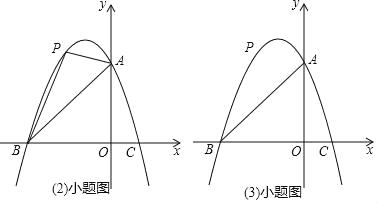
【题目】已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com