
【题目】已知函数y=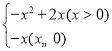 的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为_____.
的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为_____.

【答案】0<m<![]()
【解析】
由直线y=x+m与该图象恰有三个不同的交点可知直线y=x+m与y=-x(x≤0)有一个交点,与y=-x2+2x有两个交点,分别联立两个解析式求出m的取值范围即可得答案.
∵直线y=x+m与该图象恰有三个不同的交点,
∴直线y=x+m与y=-x(x≤0)有一个交点,与y=-x2+2x(x>0)有两个交点,
x+m=-x
x=![]() ,
,
∵x≤0,
∴m≥0,
-x2+2x=x+m,
x2-x+m=0,
∵y=x+m与y=-x2+2x(x>0)有两个交点,
∴△=(-1)2-4m>0,
解得:m<![]() ,
,
∵当m=0时,直线y=x+m过(0,0)点,
∴与y=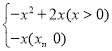 图象只有两个交点,
图象只有两个交点,
∴m≠0,
∴m的取值范围为:0<m<![]() .
.
故答案为:0<m<![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c,函数值y与自变量x之间的部分对应值如下表:
x | … | ﹣4 | ﹣1 | 0 | 1 | … |
y | … | ﹣2 | ﹣1 | ﹣2 | ﹣7 | … |
(1)此二次函数图象的对称轴是直线,此函数图象与x轴交点个数为 .
(2)求二次函数的函数表达式;
(3)当﹣5<x<﹣1时,请直接写出函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423)

查看答案和解析>>
科目:初中数学 来源: 题型:
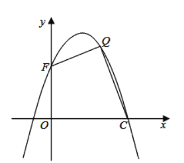
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()

(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在公园有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() 公分.敏敏观察到高度
公分.敏敏观察到高度![]() 公分矮圆柱的影子落在地面上,其影长为
公分矮圆柱的影子落在地面上,其影长为![]() 公分;而高圆柱的部分影子落在墙上,如图所示.
公分;而高圆柱的部分影子落在墙上,如图所示.

已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为![]() 公分,且此刻她的影子完全落在地面上,则影长为多少公分?
公分,且此刻她的影子完全落在地面上,则影长为多少公分?
(2)若同一时间量得高圆柱落在墙上的影长为![]() 公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平方运算和开方运算是互逆运算,如:![]() ,那么
,那么![]() ,那么如何将双重二次根式
,那么如何将双重二次根式![]()
![]() 化简呢?如能找到两个数
化简呢?如能找到两个数![]()
![]() ,使得
,使得![]() 即
即![]() ,且使
,且使![]() 即
即![]() ,
,
那么![]()
![]() ,双重二次根式得以化简;
,双重二次根式得以化简;
例如化简:![]() ;
; ![]() 且
且![]() ,
,![]()
![]()
由此对于任意一个二次根式只要可以将其化成![]() 的形式,且能找到
的形式,且能找到![]() 使得
使得![]() ,且
,且![]() ,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
(1)填空:![]() _________________;
_________________; ![]() __________________;
__________________;
(2)化简:① ![]() ②
②![]()
(3)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,能更多让利于顾客并且商家平均每天能赢利1200元.
(2)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com