练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线(a>0)过A(3,),B(4,)两点,则、之间的关系是_______________．（用“<”号连接）

    【答案】y1<y2.

    【解析】

    由于抛物线y=ax2+c（a＞0）过A（-3，y1）、B（4，y2）两点，则把A（-3，y1）、B（4，y2）分别代入y=ax2+c得，y1=9a+c，y2=16a+c，然后计算y1-y2=y1=（9a+c）-（16a+c）=-7a，而a＞0，即可得到y1与y2的大小关系．

    把A(3,y1)、B(4,y2)分别代入y=ax2+c得，

    y1=9a+c，y2=16a+c，

    ∴y1y2=y1=(9a+c)(16a+c)=7a，

    ∴a>0，

    ∴y1y2<0，即y1<y2.

    故答案为：y1<y2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列二次根式中，属于最简二次根式的是（　 　）.

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展．阜阳市某家快递公司，2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件．现假定该公司每月投递的快递总件数的增长率相同．

    (1)求该快递公司投递快递总件数的月平均增长率？

    (2) 如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的y与x的部分对应值如表：

    x

    1

    0

    2

    3

    4

    y

    5

    0

    4

    3

    0

    下列结论：①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(,2),B(,3)是抛物线上两点,则,其中正确的个数是 ( )

    A. 2B. 3C. 4D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在平面直角坐标系中,以点M(0,)为圆心,以长为半径作M交x轴于A.B两点，交y轴于C.D两点，连接AM并延长交M于P点，连接PC交x轴于E.

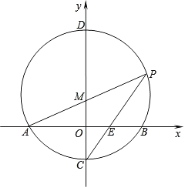
    (1)求点C.P的坐标；

    (2)求证：BE=2OE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系，经过市场调查获得部分数据如下表：

    销售价格x(元/千克)

    30

    35

    40

    45

    50

    日销售量p(千克)

    600

    450

    300

    150

    0

    (1)请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式；

    (2)求日销售利润W与X之间的函数表达式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

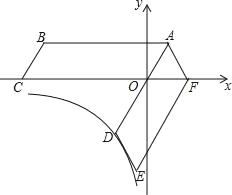
    【题目】如图，四边形ABCO是平行四边形，OA=2，AB=6，点C在x轴的负半轴上，将平行四边形 ABCO绕点A逆时针旋转得到平行四边形ADEF，AD经过点O，点F恰好落在x轴的正半轴上．若点D在反比例函数y=（x＜0）的图象上，则k的值为（　　）

    A.4B.12C.8D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数y＝的图象如图所示，若直线y＝x+m与该图象恰有三个不同的交点，则m的取值范围为_____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料题：

    浙教版九上作业本①第18页有这样一个题目：已知，如图一，P是正方形ABDC内一点，连接PA、PB、PC，若PC=2，PA=4，∠APC=135°，求PB的长.

    小明看到题目后，思考了许久，仍没有思路，就去问数学老师，老师给出的提示是：将△PAC绕点A顺时针旋转90°得到△P'AB，再利用勾股定理即可求解本题. 请根据数学老师的提示帮小明求出图一中线段PB的长为 .

    （方法迁移）：已知：如图二，△ABC为正三角形，P为△ABC内部一点，若PC=1，PA=2，PB=,求∠APB的大小.

    （能力拓展）：已知：如图三，等腰三角形ABC中∠ACB=120°，D、E是底边AB上两点且∠DCE=60°，若AD=2，BE=3，求DE的长.

    查看答案和解析>>

    同步练习册答案