
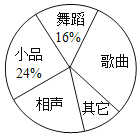
����Ŀ��ijУΪ����ף������ʮ���꣬�����ٰ�һ̨�������ᣬΪ���˽�ѧ����ϲ���Ľ�Ŀ��ʽ�������ȡ�˲���ѧ�����е��飬�涨ÿ�˴��������������赸������СƷ�������������������������ѡ����ѡ��һ�����������������Ƴ�����������������ͳ��ͼ���������ͼ����Ϣ����������⣺
��ϲ���Ľ�Ŀ | ���� |
���� | 15 |
�赸 | a |
СƷ | 12 |
���� | 10 |
���� | b |
��1���ڴ˴ε����У���Уһ���������� ����ѧ����
��2��a���� ����b���� ����
��3�������μ�ͼ�У��������������������ε�Բ�ĽǵĶ�����
��4������У����1200��ѧ�������������ϲ������������ѧ����������
���𰸡���1��50����2��8��5����3��108������4��240��.
��������
��1���ӱ����ͳ��ͼ�п��Եõ�ϲ����СƷ��������Ϊ12�ˣ�ռ����������24%�����������������
��2���赸ռ50�˵�16%�������a��ֵ���������������м�ȥ������������õ�b��ֵ��
��3���ȼ�������������ռ�İٷֱȣ���360��ȥ�˼��ɣ�
��4�������������壬������ϲ�����������İٷֱȹ�������İٷֱȣ��������������
��1��12��24%��50��
�ʴ�Ϊ50��
��2��a��50��16%��8�ˣ�
b��50��15��8��12��10��5�ˣ�
�ʴ�Ϊ��8��5��
��3��360���![]() ��108��
��108��
�����������������ε�Բ�ĽǵĶ���Ϊ108����
��4��1200��![]() ��240��
��240��
�𣺸�У1200��ѧ������ϲ������������ѧ����Լ��240�ˣ�


 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��k��8����ͼ����A��1��6����
��k��8����ͼ����A��1��6����
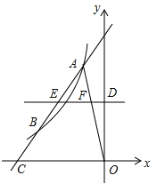
��1����k��ֵ��
��2����ͼ������A��ֱ��AC�뺯��![]() ��ͼ���ڵ�B����x�ύ�ڵ�C����AB=2BC����ֱ��AC�Ľ���ʽ��
��ͼ���ڵ�B����x�ύ�ڵ�C����AB=2BC����ֱ��AC�Ľ���ʽ��
��3���ڣ�2���������£�����OA����y����������ϵ�һ��D��ֱ��DE��x�ᣬ�ֱ��߶�AC��OA�ڵ�E��F������AEF�����Ϊ![]() �����D�����꣮
�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
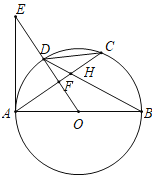
����Ŀ����ͼ��AB��![]() ��ֱ����C��
��ֱ����C��![]() ��һ�㣬D��
��һ�㣬D��![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬AE��
�ӳ�����һ�㣬AE��![]() ��A��AC��BD���ڵ�H����OE���ڵ�F������EC��
��A��AC��BD���ڵ�H����OE���ڵ�F������EC��
��1����֤��EC��![]() �����ߣ�
�����ߣ�
��2����DH=9��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
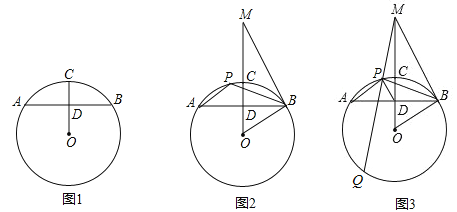
����Ŀ����2017������ʡ�������У���26�⣬10�֣���֪��AB�ǡ�O���ң���C��![]() ���е㣬����OB��OC��OC��AB�ڵ�D��
���е㣬����OB��OC��OC��AB�ڵ�D��
��1����ͼ1����֤��AD=BD��
��2����ͼ2������B����O�����߽�OC���ӳ����ڵ�M����P��![]() ��һ�㣬����AP��BP����֤����APB����OMB=90�㣻
��һ�㣬����AP��BP����֤����APB����OMB=90�㣻
��3����ͼ3���ڣ�2���������£�����DP��MP���ӳ�MP����O�ڵ�Q����MQ=6DP��sin��ABO=![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PBΪ��O�����ߣ�BΪ�е㣬ֱ��PO�����ڵ�E��F������B��PO�Ĵ���BA������Ϊ��D������O�ڵ�A���ӳ�AO����O���ڵ�C������BC��AF��
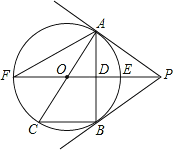
��1����֤��ֱ��PAΪ��O�����ߣ�
��2����̽���߶�EF��OD��OP֮��ĵ�����ϵ��������֤����
��3����BC=6��tan��F=![]() ����cos��ACB��ֵ���߶�PE�ij���
����cos��ACB��ֵ���߶�PE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2+bx+2��ͼ����x���ཻ�ڵ�A����1��0����B��4��0������y���ཻ�ڵ�C��

��1����ú����ı���ʽ��
��2����PΪ�ú����ڵ�һ�����ڵ�ͼ����һ�㣬����P��PQ��BC������Ϊ��Q������PC��
�����߶�PQ�����ֵ��
�����Ե�P��C��QΪ��������������ABC���ƣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ߵ깺����A��B���ֲ�ͬ�IJ�ߣ�1��A�ֲ�ߺ�2��B�ֲ�߹���250Ԫ��3��A�ֲ�ߺ�4��B�ֲ�߹���600Ԫ��
��1����A��B���ֲ��ÿ�Ľ��۷ֱ��Ƕ���Ԫ��
��2�����ڲ�߳�������ߵ����ٹ���A��B���ֲ�߹�80�ף�����ν���ʱ��������A�ֲ��ÿ���������8%����B�ֲ��ÿ�װ���һ�ν��۵İ��ۣ�����ߵ걾�ν�����Ǯ��������6240Ԫ�������ɽ�A�ֲ���ף�
��3��������һ��A�ֲ�߿ɻ���30Ԫ������һ��B�ֲ���ɻ���20Ԫ���ڣ�2���������£���ν�����ʹ���ι����������ࣿ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������3 000Ԫ����ij�ָɹ����ۣ���������״�����ã������ֵ���9 000Ԫ�������ָɹ�������εĽ��۱ȵ�һ�εĽ��������20%�������ɹ������ȵ�һ�ε�2������300 kg.������а�9Ԫ/kg�ļ۸���ۣ����ָɹ��۳������µ�600 kg���ۼ۵İ������꣮
(1)���ָɹ���һ�εĽ����Ƕ��٣�
(2)�����������ָɹ���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ABCD�У���O�ǶԽ���AC���е㣬��P���߶�AO�ϣ������A��O�غϣ���һ�����㣬����P��PE��PB��PE����CD�ڵ�E��
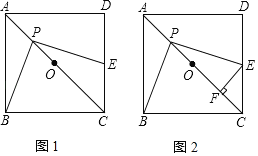
��1����֤��PE��PB��
��2����ͼ2����������ABCD�ı߳�Ϊ2������E��EF��AC�ڵ�F���ڵ�P�˶��Ĺ����У�PF�ij����Ƿ����仯�������䣬�������������ֵ�����仯����˵�����ɣ�
��3���õ�ʽ��ʾ�߶�PC��PA��CE֮���������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com