
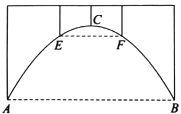
【题目】如图,是某座抛物线型的隧道示意图,已知路面AB宽24米,抛物线最高点C到路面AB的距离为8米,为保护来往车辆的安全,在该抛物线上距路面AB高为6米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.
【答案】12m.
【解析】
利用待定系数法求得抛物线的解析式,已知抛物线上距水面AB高为6米的E、F两点,可知E、F两点纵坐标为6,把y=6代入抛物线解析式,可求E、F两点的横坐标,根据抛物线的对称性求EF长.
解:如图,
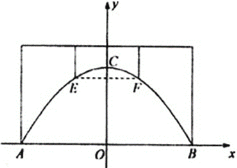
以AB所在直线为x轴、线段AB的中垂线为y轴建立直角坐标系,由题意知,A(-12,0),B(12,0),C(0,8).
设过点A、B、C的抛物线解析式为:
y=ax2+8(a<0).
把点B(12,0)的坐标代入,得a×122+8=0
解得:a=![]() ,
,
则该抛物线的解析式为:![]()
把y=6代入,得![]() ,
,
解得x1=6,x2=-6.
所以两盏警示灯之间的水平距离为:EF=|x1-x2|=|6-(-6)|=12(m).


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是直线___________,顶点坐标是___________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内画出该抛物线的图像;


(3)根据图像回答,![]() 有实数根,此时
有实数根,此时![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
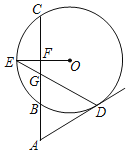
(1)求证明:AD是⊙D的切线;
(2)若∠A=60°,⊙O的半径为4,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为
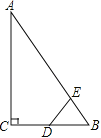
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
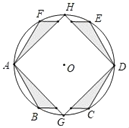
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )
A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
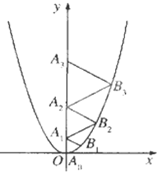
【题目】二次函数![]() 的图象如图所示,点
的图象如图所示,点![]() 位于坐标原点O,
位于坐标原点O, ![]() 在y轴的正半轴上,点
在y轴的正半轴上,点![]() 在二次函数
在二次函数![]() 第一象限的图象上,若△
第一象限的图象上,若△![]() ,△
,△![]() ,△
,△![]() …,都为等边三角形,则点
…,都为等边三角形,则点![]() 的坐标为_____
的坐标为_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com