
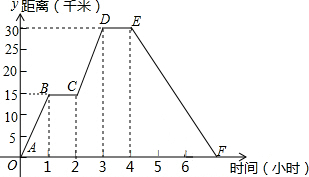
 小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.分析 (1)根据分段函数的图象上点的坐标的意义可知:小明到达离家最远的地方需3小时;此时,他离家30千米;
(2)分别利用待定系数法求得过E、F两点的直线解析式,以及A、B两点的直线解析式.分别令y=12,求解x;
(3)因为C(2,15)、D(3,30)在直线上,运用待定系数法求出解析式后,把x=2.5代入解析式即可.
解答 解:(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米;
(2)设过E、F两点的直线解析式为y=k2x+b2,
由E(4,30)、F(7,0),代入得y=-15x+90,(4≤x≤6)
过A、B两点的直线解析式为y=k3x,∵B(1,15)∴y=15x(0≤x≤1)
分别令y=12,得x=$\frac{26}{5}$(小时),x=$\frac{4}{5}$(小时)
答:小明出发$\frac{26}{5}$小时或$\frac{4}{5}$小时距家12千米;
(3)设直线CD的解析式为y=k1x+b1,由C(2,15)、D(3,30),
代入得:y=15x-15,(2≤x≤3)
当x=2.5时,y=22.5(千米)答:出发两个半小时,小明离家22.5千米.
点评 主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
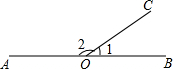 如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )| A. | $\frac{1}{2}$∠2-∠1 | B. | $\frac{1}{2}$(∠2-∠1) | C. | $\frac{1}{2}$∠2-$\frac{3}{2}$∠1 | D. | $\frac{1}{3}$(∠2+∠1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 所有的正比例函数肯定是一次函数 | |
| B. | 一次函数的一般形式是y=kx+b | |
| C. | 正比例函数和一次函数的图象都是直线 | |
| D. | 正比例函数的图象是一条过原点的直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1,0,1 | B. | 0,1,2 | C. | -2,-1,0 | D. | 1,2,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com