解不等式:2x-3≤5(x-3) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

18．解不等式：2x-3≤5（x-3）

分析去括号，移项，合并同类项，系数化成1即可．

解答解：2x-3≤5（x-3），
2x-3≤5x-15，
2x-5x≤-15+3，
-3x≤-12，
x≥4．

点评本题考查了解一元一次不等式的应用，能正确运用不等式的基本性质进行计算是解此题的关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

8．

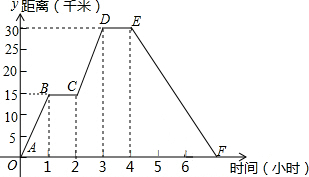小明同学骑自行车去郊外春游，下图表示他离家的距离y（千米）与所用的时间x（小时）之间关系的函数图象．
（1）根据图象回答：小明到达离家最远的地方需几小时？此时离家多远？
（2）求小明出发多长时间距家12千米？
（3）求小明出发两个半小时离家多远？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．

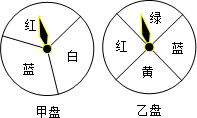张老师为了激发学生的学习兴趣，设计一个“配紫色”游戏．如图是两个可以自由转动的转盘，每个转盘被分成大小相等的几个扇形．转盘甲中的扇形分别涂有红、蓝、白三种颜色，转盘乙中的扇形分别涂有黄、绿、蓝、红四种颜色．游戏者同时转动两个转盘，如果转盘停止后，一个转盘的指针指向红色，另一个转盘的指针指向蓝色，那么红色和蓝色在一起就配成了紫色（若指针指向扇形的分界线，则需重新转动）．
（1）利用列表的方法表示游戏所有可能出现的结果；
（2）配成了紫色的概率是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．阅读材料，解答问题：
我们可以利用解二元一次方程组的代入消元法解形如$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=10①}\\{2x-y=5②}\end{array}\right.$的二元二次方程组，实质是将二元二次方程组转化为一元一次方程或一元二次方程来求解．其解法如下：
解：由②得：y=2x-5 ③
将③代入①得：x²+（2x-5）²=10
整理得：x²-4x+3=0，解得x₁=1，x₂=3
将x₁=1，x₂=3代入③得y₁=1×2-5=-3，y₂=2×3-5=1
∴原方程组的解为$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=-3}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-1}\end{array}\right.$．
（1）请你用代入消元法解二元二次方程组：$\left\{\begin{array}{l}{2x-y=3①}\\{{y}^{2}-4{x}^{2}+6x-3=0②}\end{array}\right.$；
（2）若关x，y的二元二次方程组$\left\{\begin{array}{l}{2x+y=1①}\\{a{x}^{2}+{y}^{2}+2x+1=0②}\end{array}\right.$有两组不同的实数解，求实数a的取信范围．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．在平面直角坐标系中，点坐标为（-3，4），则P点所在象限是（　　）

A．

第一象限

B．

第二象限

C．

第三象限

D．

第四象限

查看答案和解析>>