
分析 (1)根据“友好数”的定义说明即可;
(2)先根据三位数$\overline{xyz}$是“和平数”,得出y=x+z.再由$\overline{xyz}$是“友好数”,得出10x+y+10y+x+10x+z+10z+x+10y+z+10z+y=100x+10y+z,化简即为12y=78x-21z.把y=x+z代入,整理即可得出z=2x.
解答 (1)解:123不是“友好数”.理由如下:
∵12+21+13+31+23+32=132≠123,
∴123不是“友好数”;
(2)证明:∵三位数$\overline{xyz}$是“和平数”,
∴y=x+z.
∵$\overline{xyz}$是“友好数”,
∴10x+y+10y+x+10x+z+10z+x+10y+z+10z+y=100x+10y+z,
∴22x+22y+22z=100x+10y+z,
∴12y=78x-21z.
把y=x+z代入,得12x+12z=78x-21z,
∴33z=66x,
∴z=2x.
点评 本题考查了分解因式的实际运用,学生的阅读理解能力以及知识的迁移能力,解题的关键是理解“友好数”与“和平数”的定义.


科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{4}{3}$ | B. | m≥4 | C. | m<4 | D. | m≤$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.15×106 | B. | 0.115×106 | C. | 11.5×104 | D. | 1.15×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
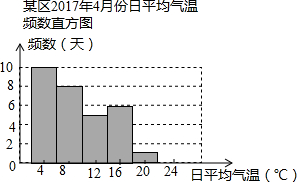 如图为某区2017年4月份日平均气温频数直方图.
如图为某区2017年4月份日平均气温频数直方图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 批发价(元) | 零售价(元) | |
| 黑色文化衫 | 10 | 25 |
| 白色文化衫 | 8 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com