
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、排球、其它等四个方面调查了若干名学生,并绘制成“折线统计图”与“扇形统计图”.请你根据图中提供的部分信息解答下列问题:
(1)在这次调查活动中,一共调查了多少名学生?
(2)求“足球”所在扇形的圆心角的度数;
(3)补全折线统计图;
(4)若已知该校有1000名学生,请你根据调查的结果估计爱好“足球”的学生共有多少人?

【答案】(1)这次调查活动中,一共调查了100名学生;(2)108°;(3)见解析;(4)爱好“足球”的学生共有300人
【解析】
(1)根据统计图中排球的人数和它所占的百分比可以求得本次调查的学生数;
(2)根据统计图中的数据可以求得“足球”所在扇形的圆心角的度数;
(3)根据(1)中的结果和统计图中的数据可以求得爱好足球和篮球的人数,从而可以将折线统计图补充完整;
(4)根据统计图中的数据可以求得爱好“足球”的学生共有多少人.
(1)40÷40%=100(名),
即在这次调查活动中,一共调查了100名学生;
(2)“足球”所在扇形的圆心角的度数是:360°×(1﹣20%﹣40%﹣![]() ×100%)=108°;
×100%)=108°;
(3)爱好的篮球的有:100×20%=20(名),
爱好足球的有:100﹣20﹣40﹣10=30(名),
补全的折线统计图如右图所示;
(4)1000×![]() =300(人),
=300(人),
答:爱好“足球”的学生共有300人.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为两人对抗赛,即把四种比赛项目写在4张完全相同的卡片上,比赛时,比赛的两人从中随机抽取1张卡片作为自己的比赛项目(不放回,且每人只能抽取一次)比赛时,小红和小明分到一组.(1)小明先抽取,那么小明抽到唐诗的概率是多少?
(2)小红擅长唐诗,小红想:“小明先抽取,我后抽取”抽到唐诗的概率是不同的,且小明抽到唐诗的概率更大,若小红后抽取,小红抽中唐诗的概率是多少?小红的想法对吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.
(1)在图1中确定点C(点C在小正方形的顶点上),画出三角形ABC,使tanB=1,△ABC的面积为10;
(2)在图2中确定点D(点D在小正方形的顶点上),画出三角形ABD,使△ABD是以AB为斜边的直角三角形,且AD>BD,直接写出∠DAB的余弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2018年初中毕业体育考试的成绩统计如表
成绩(分) | 85 | 89 | 92 | 94 | 95 | 98 | 99 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 6 | 7 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学
B. 该班学生这次考试成绩的众数是95分
C. 该班学生这次考试成绩的中位数是95分
D. 该班学生这次考试成绩的平均数是95
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在
在![]() 轴的正半轴上,以
轴的正半轴上,以![]() 为斜边向上作等腰直角
为斜边向上作等腰直角![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,动点![]() 从点
从点![]() 出发以每秒1个单位长度的速度沿
出发以每秒1个单位长度的速度沿![]() 轴的正半轴运动,设运动时间为
轴的正半轴运动,设运动时间为![]() 秒,连接
秒,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子来表示
的式子来表示![]() ;
;
(3)如图3,在(2)的条件下,当点![]() 在
在![]() 的延长线上时,点
的延长线上时,点![]() 在直线
在直线![]() 的下方,且
的下方,且![]() ,
,![]() .连接
.连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
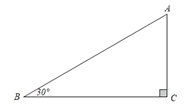
【题目】我们曾学过定理“在直角三角形中,如果一个锐角等于![]() ,那么它所对的直角边等于斜边的一半”,其逆命题也是成立的,即“在直角三角形中,如果一直角边等于斜边的一半,那么该直角边所对的角为
,那么它所对的直角边等于斜边的一半”,其逆命题也是成立的,即“在直角三角形中,如果一直角边等于斜边的一半,那么该直角边所对的角为![]() ”.如图,在
”.如图,在![]() 中,
中,![]() ,如果
,如果![]() ,那么
,那么![]() .
.
请你根据上述命题,解决下面的问题:

(1)如图1,![]() ,
,![]() 为格点,以
为格点,以![]() 为圆心,
为圆心,![]() 长为半径画弧交直线
长为半径画弧交直线![]() 于点
于点![]() ,则
,则![]() ______
______![]() ;
;
(2)如图2,![]() 、
、![]() 为格点,按要求在网格中作图(保留作图痕迹)。
为格点,按要求在网格中作图(保留作图痕迹)。
作![]() ,使点
,使点![]() 在直线
在直线![]() 上,并且
上,并且![]() ,
,![]() .
.
(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内一点,
内一点,![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于52棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
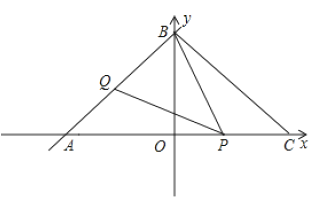
【题目】如图,一次函数![]() 的图象与
的图象与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.动点
轴对称.动点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上(点
上(点![]() 与点
与点![]() ,
,![]() 不重合),且满足
不重合),且满足![]() .
.
(1)求点![]() ,
,![]() 的坐标及线段
的坐标及线段![]() 的长度;
的长度;
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由;
,说明理由;
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com