
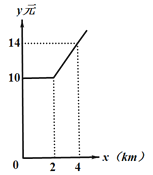
【题目】重庆出租车计费的方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图像解答下列问题:
(1)该地出租车起步价是______元;
(2)当x>2时,求y与x之间的关系式;
(3)若某乘客一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结OC、FG,则下列结论:①AE=BD;②AG=BF;③![]() ; ④图中共有4对全等三角形,其中正确结论的个数( )
; ④图中共有4对全等三角形,其中正确结论的个数( )
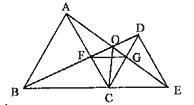
A. 3个 B. 2个 C. 1个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
组别 | 分组 | 频数(人数) | 频率 |
1 | 10≤t<30 | 0.16 | |
2 | 30≤t<50 | 20 | |
3 | 50≤t<70 | 0.28 | |
4 | 70≤t<90 | 6 | |
5 | 90≤t<110 |
(1)将表中空格处的数据补全,完成上面的频数、频率分布表;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( )
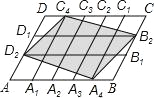
A. 2 B. ![]() C.
C. ![]() D. 15
D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
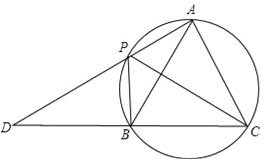
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com