
【题目】已知二次函数y=ax2+bx+c的图象经过点A(-1,0),B(1,4),C(0,3).
(1)求出此二次函数的表达式,并把它化成![]() 的形式;
的形式;
(2)请在坐标系内画出这个函数的图象,并根据图象写出函数值y为负数时,自变量x的取值范围.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
1)设函数解析式为y=ax2+bx+c,将A(-1,0),B(1,4),C(0,3)分别代入解析式,得到三元一次方程组,求解即可得二次函数的一般式;再用配方法得到顶点式;
(2)求出顶点坐标、图象与x轴、y轴的交点,连接各点,即可得到函数的图象.
(1)(1)将A(-1,0),B(1,4),C(0,3)分别代入解析式y=ax2+bx+c,得,
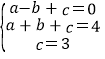 ,解得,
,解得,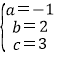 ,
,
则函数解析式为y=-x2+2x+3.
即y=-(x2-2x-3)=-(x2-2x+1-4)=-(x-1)2+4;
(2)根据y=-(x-1)2+4可知,
其顶点坐标为(1,4),
又当y=0时,-x2+2x+3=0,
x1=-1,x2=3.
则图象与x轴的交点坐标为(-1,0),(3,0).
当x=0时,y=3.
故函数图象与y轴的交点为(0,3).故可得函数图象为:


科目:初中数学 来源: 题型:
【题目】小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形面积S最大?最大面积是多少?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
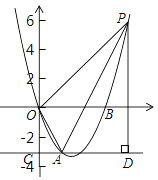
【题目】如图,已知抛物线![]() 过点A(
过点A(![]() ,-3) 和B(3
,-3) 和B(3![]() ,0),过点A作直线AC//x轴,交y轴与点C.
,0),过点A作直线AC//x轴,交y轴与点C.
(1)求抛物线的解析式;
(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D,连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;
(3)抛物线上是否存在点Q,使得![]() ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
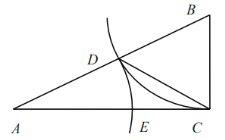
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,以A为圆心,AD长为半径画弧,交边AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=a,AC=b.
①线段AD的长是方程![]() 的一个根吗?为什么?
的一个根吗?为什么?
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出_____只粽子,利润为_____元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
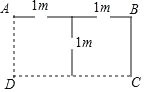
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
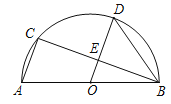
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两个点,且D是弧BC的中点,OD与BC交于点E,连接AC.
(1)若∠A=70°,求∠CBD的度数;
(2)若DE=2,BC=6,求半圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com