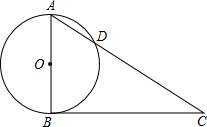
解:(1)在Rt△ABC中;
∵BC
2=AC
2-AB
2=13
2-5
2=144,
∴BC=12;
又∵∠B=90°,OB是半径,AB=5,OB=2.5,
∴BC是⊙O的切线,点A在⊙O上,
∴根据切割线定理有BC
2=CD•AC,
即有CD=

=

,
故CD=

;
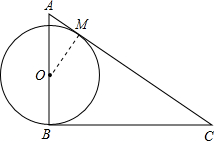
(2)当OB=2.4时,AC是⊙O的切线.,
证明如下:过O作OM⊥AC于M,
则△AOM∽△ACB,
∴
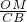
=

,OM=
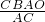
=
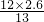
=2.4,
即O到AC的距离等于⊙O的半径,
∴当⊙O的半径为2.4时,AC是⊙O的切线.
分析:(1)先根据勾股定理求出BC的长,再根据切割线定理求出CD的长;
(2)作出辅助线OM,根据△AOM∽△ACB,利用相似三角形的性质求出OM的长,根据切线的判定定理即可证明.
点评:此题综合考查了勾股定理、切线的判定定理等内容,是一道基础性题目.

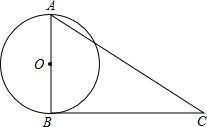 为半径作⊙O.
为半径作⊙O.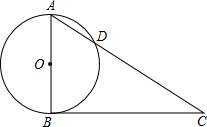 解:(1)在Rt△ABC中;
解:(1)在Rt△ABC中; =
= ,
, ;
;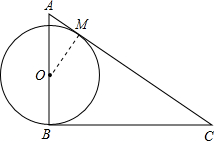
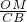 =
= ,OM=
,OM=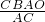 =
=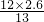 =2.4,
=2.4,
