
����Ŀ����ֱ������ϵ�У���C��ԭ��O����x���ڵ�A��2��0������y���ڵ�B��0��![]() ����
����
��1����Բ��C�����꣮
��2��������y=ax2+bx+c��O��A���㣬�Ҷ���������������y=-![]() ��ͼ���ϣ��������ߵĽ���ʽ��
��ͼ���ϣ��������ߵĽ���ʽ��
��3����Բ��C��ƽ����x���ֱ��DE������C��D��E���㣬���ж�D��E�����Ƿ��ڣ�2���е��������ϣ�
��4������2���е��������ϴ��ڵ�P��x0��y0����������APBΪ�۽ǣ���x0��ȡֵ��Χ��

���𰸡���1��Բ��C������Ϊ��1��![]() ����
����
��2�������ߵĽ���ʽΪy=![]() x2��
x2��![]() x��
x��
��3����D��E��������������
��4����1��x0��0����2��x0��3��
��������
�����������1����ͼ�߶�AB��ԲC��ֱ������Ϊ��A��B��������֪������ƽ���ߵ����ʼ�����õ�C�����ꣻ
��2����Ϊ�����߹���A��O�����Կ���öԳ��ᣬ���������ֱ��y=��![]() x�Ľ��㣬���Ƕ��κ����Ķ������꣬���ö���ʽ����һ��ʽ�����ô���ϵ����������������ߵĽ���ʽ��
x�Ľ��㣬���Ƕ��κ����Ķ������꣬���ö���ʽ����һ��ʽ�����ô���ϵ����������������ߵĽ���ʽ��
��3����ΪDE��x�ᣬ�ҹ���C�����Կɵ�D��E��������Ϊ![]() �����ֱ��AB�ij����ɵ�D��E�ĺ����꣬�������ʽ�����жϣ�
�����ֱ��AB�ij����ɵ�D��E�ĺ����꣬�������ʽ�����жϣ�
��4����ΪABΪֱ�������Ե��������ϵĵ�P����C���ڲ�ʱ��������APBΪ�۽ǣ����ԩ�1��x0��0����2��x0��3��
�����������1���ߡ�C����ԭ��O
��ABΪ��C��ֱ��
��CΪAB���е�
����C��CH��ֱx���ڵ�H������CH=![]() OB=
OB=![]() ��OH=
��OH=![]() OA=1
OA=1
��Բ��C������Ϊ��1��![]() ����
����
��2���������߹�O��A���㣬
�������ߵĶԳ���Ϊx=1��
�������ߵĶ�����ֱ��y=��![]() x�ϣ�
x�ϣ�
������������1����![]() ����
����
����������������������y=ax2+bx+c����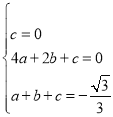 ��
��
���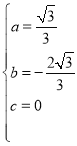 ��
��
�������ߵĽ���ʽΪy=![]() x2��
x2��![]() x��
x��
��3����OA=2��OB=2![]() ��
��
��AB=![]() =4������C�İ뾶r=2��
=4������C�İ뾶r=2��
��D��3��![]() ����E����1��
����E����1��![]() ����
����
����y=![]() x2��
x2��![]() x���飬֪��D��E�����������ϣ�
x���飬֪��D��E�����������ϣ�
��4����ABΪֱ����
�����������ϵĵ�P����C���ڲ�ʱ��������APBΪ�۽ǣ�
����1��x0��0����2��x0��3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
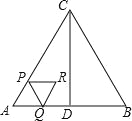
����Ŀ����ͼ����ABC�ǵȱ������Σ�AB=4cm��CD��AB�ڵ�D������P�ӵ�A��������AC��2cm/s���ٶ����յ�C�˶�������P��������P��PQ��BC������AD��DC�ڵ�Q����PQΪ�����ȱ�������PQR�����ı���APRQ����ACD�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����
��1������Q���߶�AD��ʱ���ú�t�Ĵ���ʽ��ʾQR�ij���
��2�����R�˶���·�̳���
��3������Q���߶�AD��ʱ����S��t֮��ĺ�����ϵʽ��
��4��ֱ��д���Ե�B��Q��RΪ�������������ֱ��������ʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�ա�A��B��C����AB=3����A��=30������A��B��=________����A=________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���4x2+1=4x�ĸ�������ǣ� ��
A.û��ʵ����
B.ֻ��һ��ʵ����
C.��������ȵ�ʵ����
D.����������ȵ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A=��B=90����E��AB�ϵ�һ�㣬��AE=BC����1=��2��

��1��Rt��ADE��Rt��BECȫ���𣿲�˵�����ɣ�
��2����CDE�Dz���ֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AE=CF����AFD=��CEB����ô��������һ�������������ж���ADF�ա�CBE���ǣ� ��
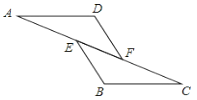
A. ��A=��C B. AD=CB C. BE=DF D. AD��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������A��O��B��Ӧ�����ֱ�Ϊ��3��0��1����PΪ����������һ�㣬���ʾ����Ϊx��
��1�������P����A����B�ľ�����ȣ���ôx=��
��2����x=ʱ����P����A����B�ľ���֮����6��
��3������P����A����B�ľ���֮����С����x��ȡֵ��Χ����
��4���������ϣ���M��N��ʾ�����ֱ�Ϊx1 �� x2 �� ���ǰ�x1 �� x2֮��ľ���ֵ������M��N֮��ľ��룬��MN=|x1��x2|��
����P��ÿ��3����λ���ȵ��ٶȴӵ�O�����˶�ʱ����E��ÿ��1����λ���ȵ��ٶȴӵ�A�����˶�����F��ÿ��4����λ���ȵ��ٶȴӵ�BҲ�����˶�����������ͬʱ��������ô�˶���ʱ����P����E����F�ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һֻ�����ڵ�һ����x�ᡢy�����������ڵ�һ���ӣ�����ԭ��������(0��1)��Ȼ����Ű�ͼ�м�ͷ��ʾ������������(0��0)��(0��1�� ��(1��1)����1��0����������ÿ������һ����λ����ô��35��ʱ��������λ�õ������ǣ� �� 
A.(4��0)
B.(5��0)
C.(0��5)
D.(5��5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȣ��±��ǽ����ܵ����������

�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨����A���ͺŵĵ��������ܲɹ�����̨��
��3���ڣ�2���������£�������������30̨������ܷ�ʵ������Ϊ1400Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com