
【题目】如图,某防洪堤坝长300米,其背水坡的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得加固后坡面的坡角∠ADB=50°
(1)求此时应将坝底向外拓宽多少米?(结果保留到0.01米)
(2)完成这项工程需要土石多少立方米?(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
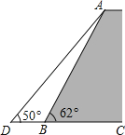
【答案】(1)应将坝底向外拓宽大约6.58米;(2)21714立方米
【解析】
(1)过A点作AE⊥CD于E.在Rt△ABE中,根据三角函数可得AE,BE,在Rt△ADE中,根据三角函数可得DE,再根据DB=DE-BE即可求解;
(2)用△ABD的面积乘以坝长即为所需的土石的体积.
解:(1)过A点作AE⊥CD于E.
在Rt△ABE中,∠ABE=62°.
∴AE=ABsin62°≈25×0.88=22米,
BE=ABcos62°≈25×0.47=11.75米,
在Rt△ADE中,∠ADB=50°,
∴DE=![]() =18.33米,
=18.33米,
∴DB=DE-BE≈6.58米.
故此时应将坝底向外拓宽大约6.58米.
(2)6.58×22×![]() ×300=21714立方米.
×300=21714立方米.


科目:初中数学 来源: 题型:
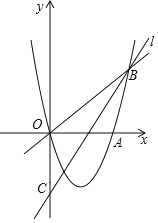
【题目】如图,抛物线y=ax2+bx+c经过O、A(4,0)、B(5,5)三点,直线l交抛物线于点B,交y轴于点C(0,﹣4).点P是抛物线上一个动点.
(1)求抛物线的解析式;
(2)点P关于直线OB的对称点恰好落在直线l上,求点P的坐标;
(3)M是线段OB上的一个动点,过点M作直线MN⊥x轴,交抛物线于点N.当以M、N、B为顶点的三角形与△OBC相似时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
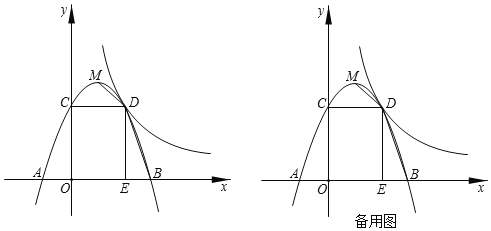
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线于另一点D,作DE⊥x轴,垂足为点E,双曲线y=![]() (x>0)经过点D,连接MD,BD.
(x>0)经过点D,连接MD,BD.
(1)求抛物线的表达式;
(2)点N,F分别是x轴,y轴上的两点,当以M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;
(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是 .
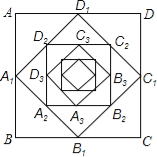
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 和抛物线
和抛物线![]() :
:![]() ,其中
,其中![]() .
.
![]() 下列说法你认为正确的序号是______;
下列说法你认为正确的序号是______;
![]() 抛物线
抛物线![]() 和
和![]() 与y轴交于同一点
与y轴交于同一点![]() ;
;
![]() 抛物线
抛物线![]() 和
和![]() 开口都向上;
开口都向上;
![]() 抛物线
抛物线![]() 和
和![]() 的对称轴是同一条直线;
的对称轴是同一条直线;
![]() 当
当![]() 时,抛物线
时,抛物线![]() 和
和![]() 都与x轴有两个交点
都与x轴有两个交点
![]() 抛物线
抛物线![]() 和
和![]() 相交于点E、F,当k的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
相交于点E、F,当k的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
![]() 在
在![]() 中,若抛物线
中,若抛物线![]() 的顶点为M,抛物线
的顶点为M,抛物线![]() 的顶点为N,问:
的顶点为N,问:
是否存在实数k,使![]() ?如存在,求出实数k;如不存在,请说明理由.
?如存在,求出实数k;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是![]() ,最低气温是
,最低气温是![]() ,则该日气温的极差是
,则该日气温的极差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
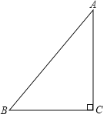
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠A≠∠B.
(1)请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)
(2)在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E;(不要求写作法,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD折叠,使点C落在点F处,线段DF与AB相交于点E.
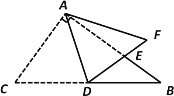
(1)求∠BDE的度数.
(2)求证:△DEB∽△ADB.
(3)若BC=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4000元购进一批某品牌的文化衫若干件,很快售完,该店又用6300元钱购进第二批这种文化衫,所进的件数比第一批多40%,每件文化衫的进价比第一批每件文化衫的进价多10元,请解答下列问题:
(1)求购进的第一批文化衫的件数;
(2)为了取信于顾客,在这两批文化衫的销售中,售价保持了一致.若售完这两批文化衫服装店的总利润不少于4100元钱,那么服装店销售该品牌文化衫每件的最低售价是多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com