
【题目】如图,△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD折叠,使点C落在点F处,线段DF与AB相交于点E.
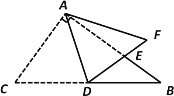
(1)求∠BDE的度数.
(2)求证:△DEB∽△ADB.
(3)若BC=4,求BE的长.
【答案】(1)36°;(2)详见解析;(3)![]()
【解析】
(1)根据三角形内角和定理求出∠C=90°-∠B=54°.由直角三角形斜边上的中线的性质得出AD=BD=CD,利用等腰三角形的性质求出∠BAD=∠B=36°,∠DAC=∠C=54°,利用三角形内角和定理求出∠ADC=180°-∠DAC-∠C=72°.再根据折叠的性质得出∠ADF=∠ADC=72°,然后根据平角的定义得出∠BDE=180°-∠ADC-∠ADF=36°.
(2)根据∠B=∠B,∠BDE=∠BAD证明即可;
(3)由△DEB∽△ADB得![]() ,设BE=x得方程x(x+2)=4,求解方程即可.
,设BE=x得方程x(x+2)=4,求解方程即可.
(1)∵在Rt△ABC中,∠BAC=90°,∠B=36°,
∴∠C=90°-∠B=54°.
∵AD是斜边BC上的中线,
∴AD=BD=CD,
∴∠BAD=∠B=36°,∠DAC=∠C=54°,
∴∠ADC=180°-∠DAC-∠C=72°.
∵将△ACD沿AD对折,使点C落在点F处,
∴∠ADF=∠ADC=72°,
∴∠BDE=180°-∠ADC-∠ADF=180°-72°-72°=36°.
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD,
∵∠B=36°,∴∠BAD=36°,
∵∠BDE=36°,
∴∠B=∠B,∠BDE=∠BAD,
∴△DEB∽△ADB.
(3)∵△DEB∽△ADB,
∴![]() ,设BE=x,
,设BE=x,
∵BC=4,
∴![]() ,
,
∴BE=x=![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,4),B(﹣4,0),C(﹣1,0).
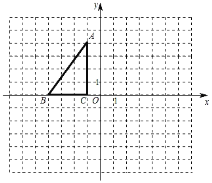
(1)△A1B1C1与△ABC关于原点O对称,画出△A1B1C1并写出点A1的坐标;
(2)△A2B2C2是△ABC绕原点O顺时针旋转90°得到的,画出△A2B2C2并写出点A2的坐标;
(3)连接OA、OA2,在△ABC绕原点O顺时针旋转90°得到的△A2B2C2的过程中,计算A变换到A2过程中的路径是多少?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
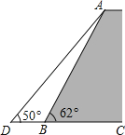
【题目】如图,某防洪堤坝长300米,其背水坡的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得加固后坡面的坡角∠ADB=50°
(1)求此时应将坝底向外拓宽多少米?(结果保留到0.01米)
(2)完成这项工程需要土石多少立方米?(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连结OD,AD.以下结论:①∠ADB=90°;②D是BC的中点;③AD是∠BAC的平分线;④OD∥AC,其中正确结论的个数有( )
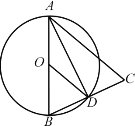
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
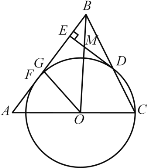
【题目】如图,在△ABC中,AB=AC=10,tan∠A=![]() ,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
(1)求证:DE是⊙O的切线;
(2)当⊙O与AB相切于点F时,求⊙O的半径;
(3)在(2)的条件下,连接OB交DE于点M,点G在线段EF上,连接GO.若∠GOM=45°,求DM和FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
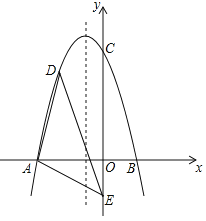
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2,2)、B(﹣3,1)、C(﹣1,0).
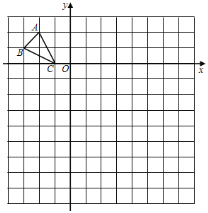
(1)将△ABC先向右平移2个单位长度,向下平移7个单位长度,得到△DEF,画出△DEF;
(2)以O为位似中心,将△ABC放大为原来的2倍,在网格内画出放大后的△A1B1C1,若P(x,y)为△ABC中的任意一点,其对应点P1的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF,
(1)求证:AE=CF;
(2)若AB=3,∠AOD=120°,求矩形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com