
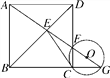
【题目】如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G,连接EC.
求证:CE是△CGF的外接圆⊙O的切线.
科目:初中数学 来源: 题型:
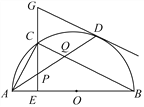
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是______(用含m的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少需要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作.根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
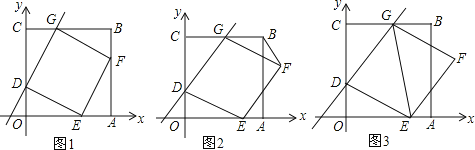
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com