练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：A（0，1），B（2，0），C（4，3）

    （1）在直角坐标系中描出各点，画出△ABC．

    （2）求△ABC的面积；

    （3）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．

    【答案】（1）画图见解析；（2）4；（3）P（10，0）或P（-6，0）；（0，5），（0，-3）

    【解析】试题分析：（1）根据坐标标出点，然后连接即可；

    （2）用梯形的面积减去两个三角形的面积即可；

    （3）根据同底等高再坐标轴上找点即可．

    试题解析：（1）如图

    （2）=4，

    （3）由P在x轴上，可由OA=1，可知PB=8，因此可知P点为（-6，0），（10，0）；如果在y轴上，则由OB=2，可知AP=4，因此可知P为（0，5），（0，-3）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形网格中，每个小正方形的边长都为1，△ABC在网格中的位置如图所示，△ABC的三个顶点都在格点上．将点A、B、C的横坐标不变，纵坐标都乘以－1，分别得到点A1、B1、C1

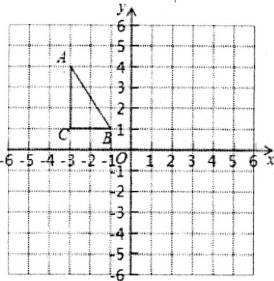
    （1）写出△A1B1C1，三个顶点的坐标________；

    （2）在图中画出△A1B1C1，则△ABC与△A1B1C1关于________对称；

    （3）若以点A、C、P为顶点的三角形与△ABC全等，直接写出所有符合条件的点P的坐标________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC=18，BC=12，正方形DEFG的顶点E，F在△ABC内，顶点D，G分别在AB，AC上，AD=AG，DG=6，则点F到BC的距离为（ ）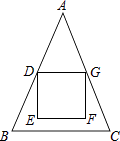
    A.1
    B.2
    C.12 ﹣6
    D.6 ﹣6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点就做格点，以格点为顶点分别按下列要求画三角形；

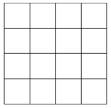
    (1)使三角形的三边长分别为2，3，

    （在图中画出一个既可）；

    (2)请在数轴上作出的对应点

    (2)如图①，A，B，C是三个格点(即小正方形的顶点)，判断AB与BC的位置关系，并说明理由；

    (3)如图②，连接三格和两格的对角线，求∠α＋∠β的度数(要求：画出示意图，并说明理由)．

    　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．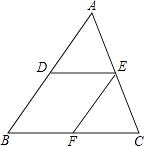
    （1）求证：四边形DBFE是平行四边形；
    （2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在精准扶贫中，某村的李师傅在县政府的扶持下，去年下半年，他对家里的3个温室大棚进行修整改造，然后，1个大棚种植香瓜，另外2个大棚种植甜瓜，今年上半年喜获丰收，现在他家的甜瓜和香瓜已全部售完，他高兴地说：“我的日子终于好了”. 最近，李师傅在扶贫工作者的指导下，计划在农业合作社承包5个大棚，以后就用8个大棚继续种植香瓜和甜瓜，他根据种植经验及今年上半年的市场情况，打算下半年种植时，两个品种同时种，一个大棚只种一个品种的瓜，并预测明年两种瓜的产量、销售价格及成本如下：

    品种

    产量(斤/每棚)

    销售量(元/每斤)

    成本(元/每棚)

    香瓜

    2000

    12

    8000

    甜瓜

    4500

    3

    5000

    现假设李师傅今年下半年香瓜种植的大棚数为x个，明年上半年8个大棚中所产的瓜全部售完后，获得的利润为y元.

    根据以上提供的信息，请你解答下列问题：

    (1)求出y与x之间的函数关系式；

    (2)求出李师傅种植的8个大棚中，香瓜至少种植几个大棚? 才能使获得的利润不低于10万元.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC．若AC=6，则四边形ABCD的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=x2+bx+c，其图象抛物线交x轴于点A（1，0），B（3，0），交y轴于点C，直线l过点C，且交抛物线于另一点E（点E不与点A、B重合）．
    （1）求此二次函数关系式；
    （2）若直线l1经过抛物线顶点D，交x轴于点F，且l1∥l，则以点C、D、E、F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由．
    （3）若过点A作AG⊥x轴，交直线l于点G，连接OG、BE，试证明OG∥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学举办运动会，在1500米的项目中，参赛选手在200米的环形跑道上进行，如图记录了跑得最快的一位选手与最慢的一位选手的跑步全过程（两人都跑完了全程），其中x代表的是最快的选手全程的跑步时间，y代表的是这两位选手之间的距离，下列说不合理的是（　　）

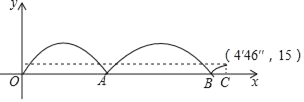
    A. 出发后最快的选手与最慢的选手相遇了两次

    B. 出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时短

    C. 最快的选手到达终点时，最慢的选手还有415米未跑

    D. 跑的最慢的选手用时4′46″

    查看答案和解析>>

    同步练习册答案