
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,如图记录了跑得最快的一位选手与最慢的一位选手的跑步全过程(两人都跑完了全程),其中x代表的是最快的选手全程的跑步时间,y代表的是这两位选手之间的距离,下列说不合理的是( )
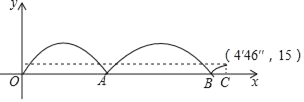
A. 出发后最快的选手与最慢的选手相遇了两次
B. 出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时短
C. 最快的选手到达终点时,最慢的选手还有415米未跑
D. 跑的最慢的选手用时4′46″
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,6)和点M(m,n)都在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,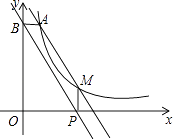
(1)k的值为;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
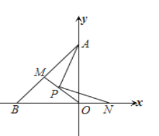
【题目】如图,在平面直角坐标系中,OA=OB,点P为△ABO的角平分线的交点,若PN⊥PA交x轴于N,延长OP交AB于M,写出AO,ON,PM之间的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2016次变换后,正方形ABCD的对角线交点M的坐标变为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距20km.甲、乙两人都由A地去B地,甲骑自行车,平均速度为10km/h;乙乘汽车,平均速度为40km/h,且比甲晚1.5h出发.设甲的骑行时间为x(h)(0≤x≤2)
(1)根据题意,填写下表:
时间x(h) 与A地的距离 | 0.5 | 1.8 | _____ |
甲与A地的距离(km) | 5 |
| 20 |
乙与A地的距离(km) | 0 | 12 |
|
(2)设甲,乙两人与A地的距离为y1(km)和y2(km),写出y1,y2关于x的函数解析式;
(3)设甲,乙两人之间的距离为y,当y=12时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15立方米的无盖长方体运输箱,且此长方体运输箱底面的长比宽多2米,现已知购买这种铁皮每平方米需20元,问购买这张矩形铁皮共花了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
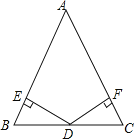
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
(1)求E点坐标;
(2)设抛物线的解析式为y=a(x﹣h)2+k,求a,h,k;
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点M,N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com