
����Ŀ��A��B�������20km���ס������˶���A��ȥB�أ��������г���ƽ���ٶ�Ϊ10km/h���ҳ�������ƽ���ٶ�Ϊ40km/h���ұȼ���1.5h�������������ʱ��Ϊx��h����0��x��2��
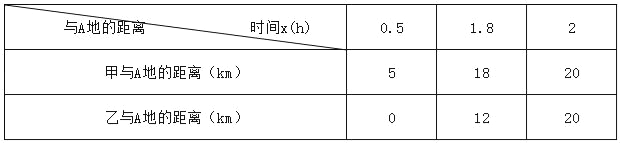
��1���������⣬��д�±���
ʱ��x��h�� ��A�صľ��� | 0.5 | 1.8 | _____ |
����A�صľ��루km�� | 5 | ���� | 20 |
����A�صľ��루km�� | 0 | 12 | ���� |
��2����ף���������A�صľ���Ϊy1��km����y2��km����д��y1��y2����x�ĺ�������ʽ��
��3����ף�������֮��ľ���Ϊy����y=12ʱ����x��ֵ��
���𰸡���1��18��2��20��2��![]() ��3����y=12ʱ��x��ֵ��1.2��1.6
��3����y=12ʱ��x��ֵ��1.2��1.6
��������
����������·�̡�ʱ�䡢�ٶ�����Ĺ�ϵͨ�����㼴�������Ӧ�𰸣�
����������·��=�ٶ���ʱ���ϼס��ҵ��ٶ��Լ�ʱ�䷶Χ������ô𰸣�
���������⣬��![]() ��Ȼ��ֱ�y=12���뼴����ô�.
��Ȼ��ֱ�y=12���뼴����ô�.
����������֪���ס��Ҷ���ƽ���ٶȷֱ���ƽ���ٶ�Ϊ10km/h��40km/h���ұȼ���1.5h������
��ʱ��x=1.8 ʱ�����뿪A�ľ�����10��1.8=18��km����
�����뿪A�ľ���20kmʱ������ʻʱ����20��10=2��ʱ����
��ʱ����ʻ��ʱ����2��1.5=0. 5��ʱ����
�������뿪A�ľ�����40��0.5=20��km����
��������
����������֪��
y1=10x��0��x��1.5����
y2=![]() ��
��
���������⣬��![]() ��
��
��0��x��1.5ʱ����10x=12����x=1.2��
��1.5��x��2ʱ���ɩ�30x+60=12����x=1.6��
��ˣ���y=12ʱ��x��ֵ��1.2��1.6.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ƶ�У�ij�����ʦ�����������ķ����£�ȥ���°��꣬���Լ����3�����Ҵ�������������죬Ȼ��1��������ֲ��ϣ�����2��������ֲ��ϣ������ϰ���ϲ����գ��������ҵ���Ϻ������ȫ�����꣬�����˵�˵�����ҵ��������ں�����. �������ʦ���ڷ�ƶ�����ߵ�ָ���£��ƻ���ũҵ������а�5������Ժ����8�����������ֲ��Ϻ���ϣ���������ֲ���鼰�����ϰ�����г�����������°�����ֲʱ������Ʒ��ͬʱ�֣�һ������ֻ��һ��Ʒ�ֵĹϣ���Ԥ���������ֹϵIJ��������ۼ۸ɱ����£�
Ʒ�� | ����(��/ÿ��) | ������(Ԫ/ÿ��) | �ɱ�(Ԫ/ÿ��) |
��� | 2000 | 12 | 8000 |
��� | 4500 | 3 | 5000 |
�ּ�����ʦ�������°��������ֲ�Ĵ�����Ϊx���������ϰ���8�������������Ĺ�ȫ�������õ�����ΪyԪ.
���������ṩ����Ϣ���������������⣺
(1)���y��x֮��ĺ�����ϵʽ��
(2)�����ʦ����ֲ��8�������У����������ֲ��������? ����ʹ��õ�������10��Ԫ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���M�� ![]() ��
�� ![]() �����Ե�MΪԲ�ģ�OM��Ϊ�뾶����M��ʹ��M��ֱ��OM����һ����Ϊ��B����x�ᣬy�����һ����ֱ�Ϊ��D��A����ͼ��������AM����P��
�����Ե�MΪԲ�ģ�OM��Ϊ�뾶����M��ʹ��M��ֱ��OM����һ����Ϊ��B����x�ᣬy�����һ����ֱ�Ϊ��D��A����ͼ��������AM����P�� ![]() �ϵĶ��㣮
�ϵĶ��㣮 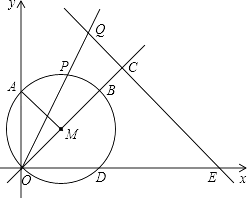
��1��д����AMB�Ķ�����
��2����Q������OP�ϣ���OPOQ=20������Q��QC��ֱ��ֱ��OM������ΪC��ֱ��QC��x���ڵ�E�� �ٵ�����P���B�غ�ʱ�����E�����ꣻ
������QD�����Q��������Ϊt����QOD�����ΪS����S��t�ĺ�����ϵʽ��S��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ٰ��˶��ᣬ��1500����Ŀ�У�����ѡ����200�Ļ����ܵ��Ͻ��У���ͼ��¼���ܵ�����һλѡ����������һλѡ�ֵ��ܲ�ȫ���̣����˶�������ȫ�̣�������x������������ѡ��ȫ�̵��ܲ�ʱ�䣬y������������λѡ��֮��ľ��룬����˵���������ǣ�������
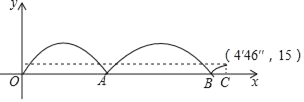
A. ����������ѡ����������ѡ������������
B. ����������ѡ����������ѡ�ֵ�һ�������ȵڶ�����������ʱ��
C. ����ѡ�ֵ����յ�ʱ��������ѡ�ֻ���415��δ��
D. �ܵ�������ѡ����ʱ4��46��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڱ߳�Ϊ1����λ���ȵ�С��������ɵ�������,������ƽ��ֱ������ϵ�������AOB.(�����������ߵĽ���)
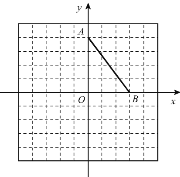
��1����������AOB��y�ᷭ�۵õ�����AOB1,���B1������Ϊ_________.
��2����������AOB������AB1����ƽ��2.5����λ�õ�����A2O2B2,���A2������Ϊ_______.
��3���������AB1B2�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���Գ�����ֱ��x=1���������ĸ����۴�����ǣ� �� 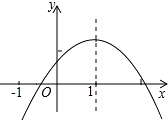
A.c��0
B.2a+b=0
C.b2��4ac��0
D.a��b+c��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=�� ![]() +bx+c��ͼ��A��2��0����B��0����6�����㣮
+bx+c��ͼ��A��2��0����B��0����6�����㣮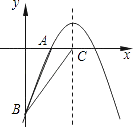
��1����������κ����Ľ���ʽ��
��2����ö��κ����ĶԳ�����x�ύ�ڵ�C������BA��BC�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ��,![]() ����
����![]() .
.
(1)��![]() ��ֵ;
��ֵ;
(2)����![]() ����������ϴ���һ��
����������ϴ���һ��![]() ��ʹ
��ʹ![]() �����
�����![]() ������;
������;
������������һ�����ڶ��ٸ���![]() ��ʹ
��ʹ![]() ����?��ֱ��д�����������ĵ�
����?��ֱ��д�����������ĵ�![]() ������.
������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com